Four different high schools in local towns took random samples of 100 students in three grades, and collected data on the weekly time spent studying to see if students in each of these grades study on average for the same amount of time per week. The four schools ran ANOVA tests on their samples, and the F-Statistics were , , , and . Which F-Statistic is most likely to indicate the average study times across grades are not all the same?
- 1. Introduction to Statistics53m
- 2. Describing Data with Tables and Graphs2h 1m
- 3. Describing Data Numerically1h 48m
- 4. Probability2h 26m
- 5. Binomial Distribution & Discrete Random Variables2h 55m
- 6. Normal Distribution & Continuous Random Variables1h 48m
- 7. Sampling Distributions & Confidence Intervals: Mean2h 8m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 20m
- 9. Hypothesis Testing for One Sample2h 23m
- 10. Hypothesis Testing for Two Samples3h 25m
- 11. Correlation1h 6m
- 12. Regression1h 4m
- 13. Chi-Square Tests & Goodness of Fit1h 30m
- 14. ANOVA1h 4m
Struggling with Statistics for Business?
Join thousands of students who trust us to help them ace their exams!Watch the first videoA marketing manager wants to evaluate whether three different advertising platforms-TV, social media, and print media-lead to different average sales performance across regional stores. She runs a 4-wook advertising campaign, assigning one platform to a group of 5 stores each (15 stores total). After the campaign, she collects the weekly soles (in $1,000s) for each store during the campaign period. She wants to determine whether there is a statistically significant difference in mean sales among the three advertising platforms. In an ANOVA test a P-value of 0.03 is obtained. What can be concluded about mean weekly sales for different advertising platforms?
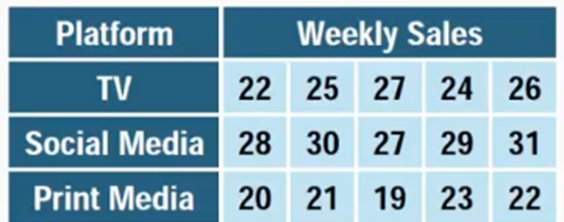
Since the P-value (0.03) is greater than the significance level (typically 0.05), we fail to reject the null hypothesis and conclude that there is no significant difference in mean sales among the platforms.
Since the P-value (0.03) is greater than 0.05, we reject the null hypothesis and conclude that there is a significant difference in the mean sales across the platforms.
Since the P-value (0.03) is less than 0.05, we fail to reject the null hypothesis and conclude that there is no significant difference in mean sales across the platforms.
Since the P-value (0.03) is less than the significance level (typically 0.05), at least one advertising platforms leads to a significant difference in average sales.
 Verified step by step guidance
Verified step by step guidance
 6:46m
6:46mWatch next
Master Introduction to ANOVA with a bite sized video explanation from Patrick
Start learning