Which of the following best describes a scatterplot?

A scatterplot shows a strong positive correlation between coffee consumption and productivity, but the data comes from a single office over one week. What should you consider before concluding coffee increases productivity?

A newspaper article says: “We found a strong correlation between the type of pet owned (dog, cat, or none) and annual income.” What is wrong with this statement, and what is a better way to write it?

A researcher is examining the relationship between the number of hours studied ($X$) and the final exam score ($Y$) of a group of students. After plotting the data on a scatter plot, the researcher observes a general upward trend. To investigate further, the researcher performs a linear regression analysis, which results in the equation $Y=50+5X$. Which of the following is the best interpretation of this regression equation?

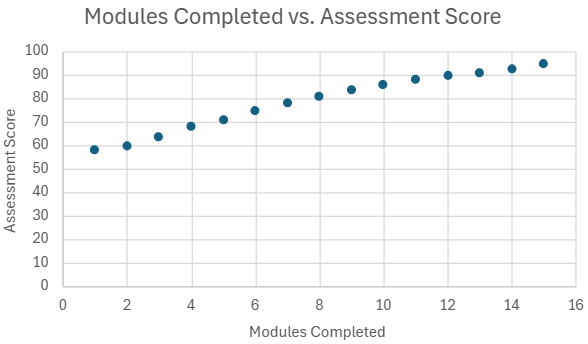
A training specialist recorded the number of online learning modules completed by $15$ employees and their performance scores on a post-training assessment (out of $100$). The scatterplot below displays the relationship between these two variables. Based on the scatterplot, what kind of linear correlation exists between the number of modules completed and the assessment scores?

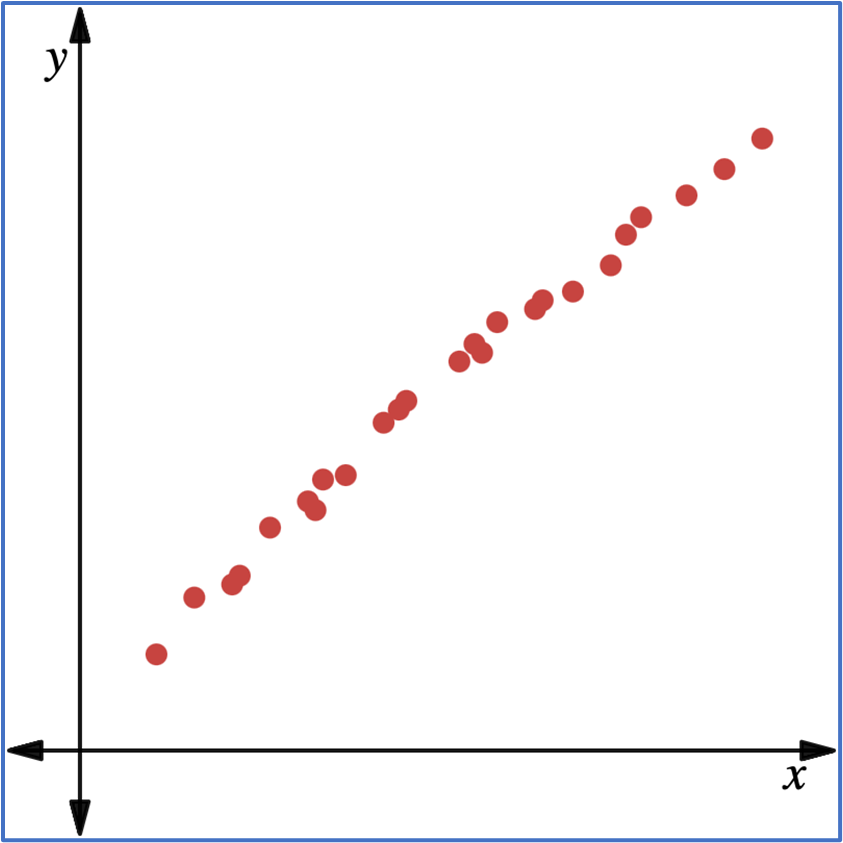
Which of the following scatterplots best represents a linear correlation?

Determine the type of linear correlation between the variables shown in the scatter plot.

A researcher records daily calories consumed and body weight for participants. Which term correctly names the variable that is explained by daily calories consumed?

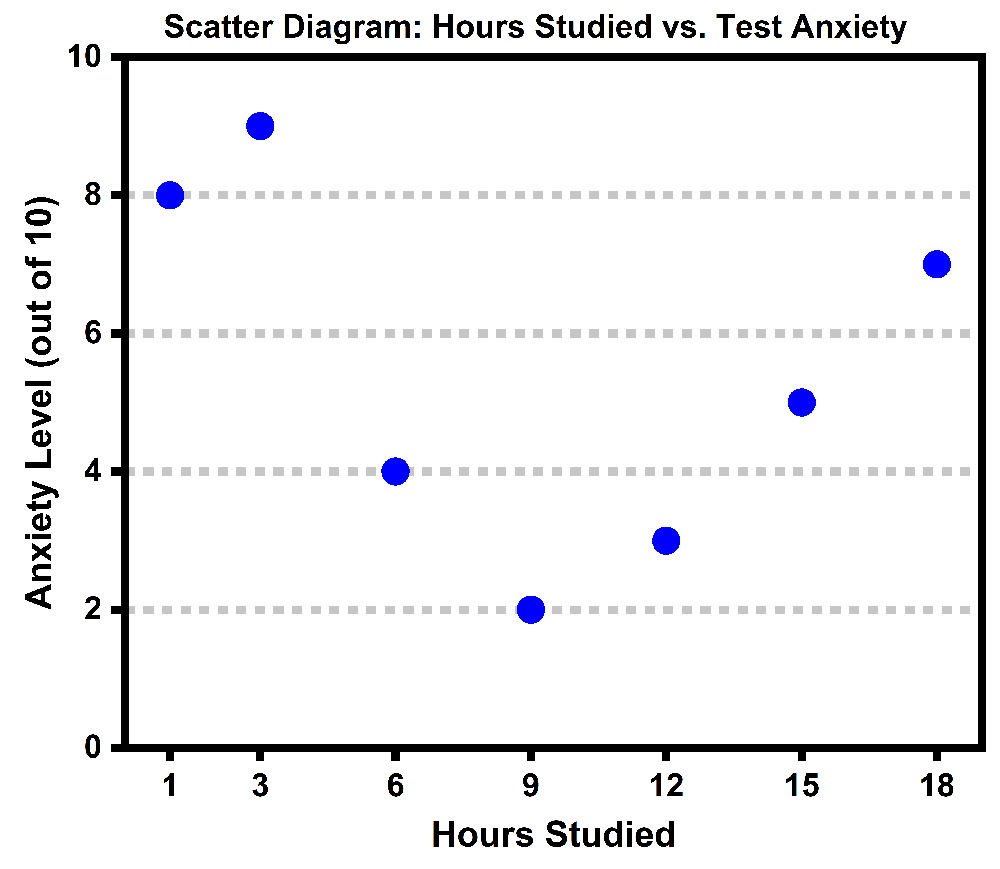
Based on the provided scatter diagram, what is wrong with the following statement: "Because the linear correlation coefficient between the number of hours studied and the self-reported anxiety level on a test day is $-0.05$, there is no relationship between study time and test anxiety."

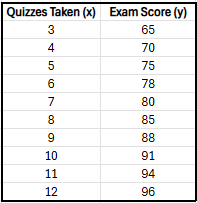
A teacher is studying the relationship between the number of practice quizzes taken and final exam scores among students in a math class. The data for $10$ students is shown below:

The correlation coefficient for this data is $r=0.98$, indicating a strong positive linear relationship. The teacher then adds data for an ${11}^{\text{th}}$ student who took only $2$ quizzes but scored $95$ on the exam. How would this new data point likely affect the correlation coefficient $r$?

The correlation coefficient for this data is $r=-0.98$, showing a strong negative linear relationship: higher body fat percentage tends to be associated with fewer push-ups.

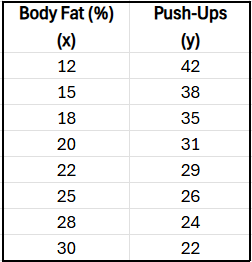
Suppose the trainer removes the data for the client with $30\%$ body fat and $22$ push-ups. How is the correlation coefficient $r$ likely to change?

If the correlation coefficient for a dataset is $r=-0.57$, what is the coefficient of determination $r^2$? How much of the variation is explained by the regression line, and how much is unexplained?

If the correlation coefficient for a dataset is $r=-0.705$, what is the value of $r^2$? What does this indicate about the explained and unexplained variation in the data?

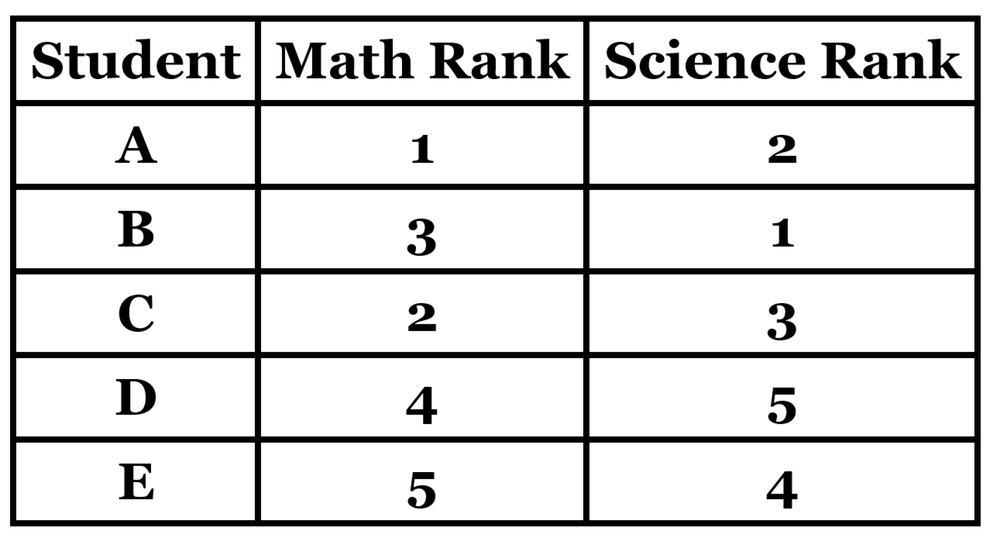
Use the ranks from the data provided below to calculate the Spearman rank correlation coefficient. Then, using a $0.05$ significance level, find the critical value and determine whether there is a statistically significant correlation between the two variables.

Suppose the Spearman rank correlation coefficient $r_s$ between two variables is calculated as $-1$. What does this imply about the relationship between the variables?