Which of the following intervals correctly represents all possible values of the Pearson correlation coefficient $r$?

What is the possible range of values for the correlation coefficient (r)?

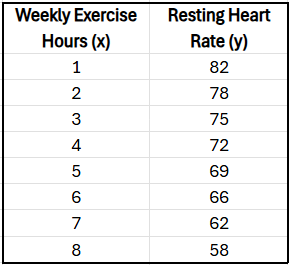
A researcher is studying the relationship between hours of weekly exercise and resting heart rate (in beats per minute) among a group of adults. The data for 8 participants is shown below:

The correlation coefficient for the data is $r=-0.99$, indicating a strong negative linear relationship: more exercise is associated with a lower resting heart rate. The researcher decides to remove the data for the participant who exercised 1 hour per week and had a heart rate of $82$. How would removing this data point most likely affect the correlation coefficient $r$?

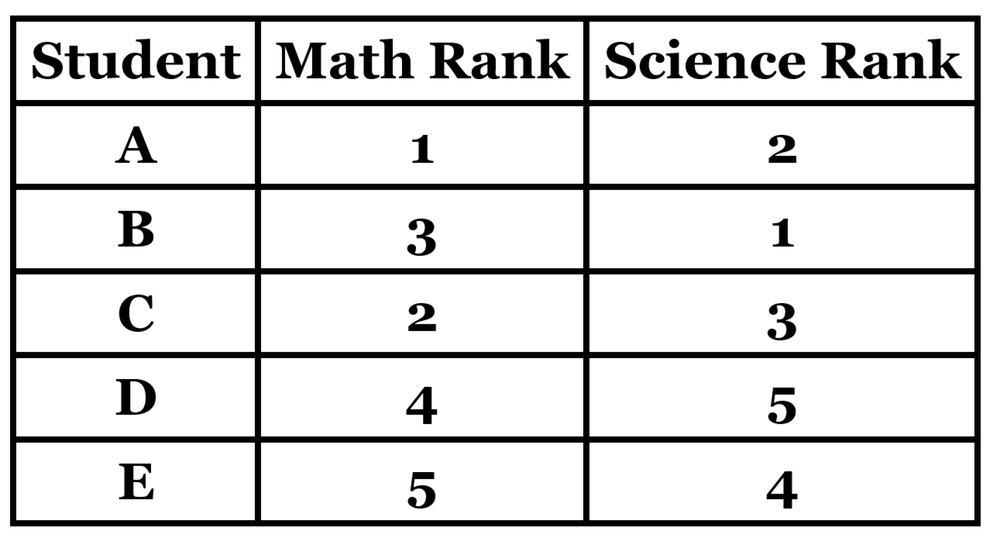
Use the ranks from the data provided below to calculate the Spearman rank correlation coefficient. Then, using a $0.05$ significance level, find the critical value and determine whether there is a statistically significant correlation between the two variables.

A study finds r = 0.78 between advertising spend and sales. According to general cutoffs, how would you classify this correlation?

A researcher calculates the Spearman rank correlation coefficient for two variables. Which of the following statements is true about the possible range of this coefficient?

A researcher finds a correlation of $0.63$ between hours of exercise per week for matched participants. What fraction of the variation in one participant's exercise hours is explained by the other's hours?

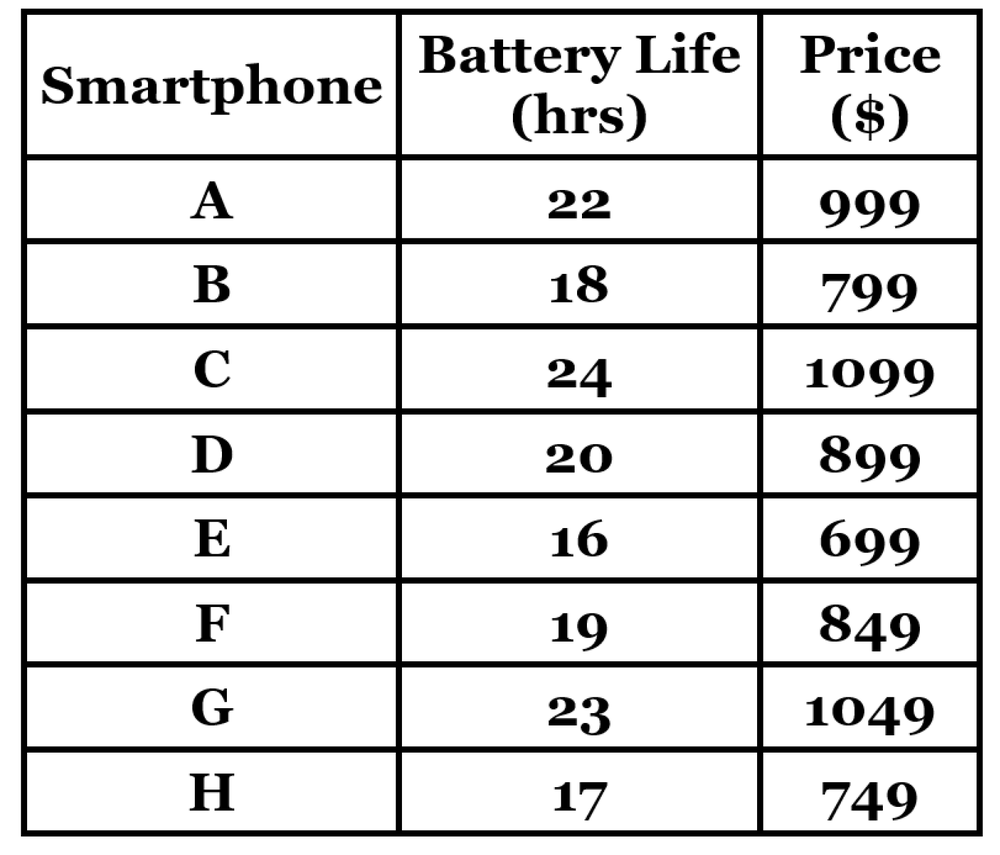
The following table lists battery life (in hours of continuous usage) and prices (in US dollars) for different smartphone models.

Use the rank correlation coefficient (Spearman’s $\rho$) to test the hypothesis of a correlation between battery life and price. Use $\alpha =0.05$. What conclusion can you draw?

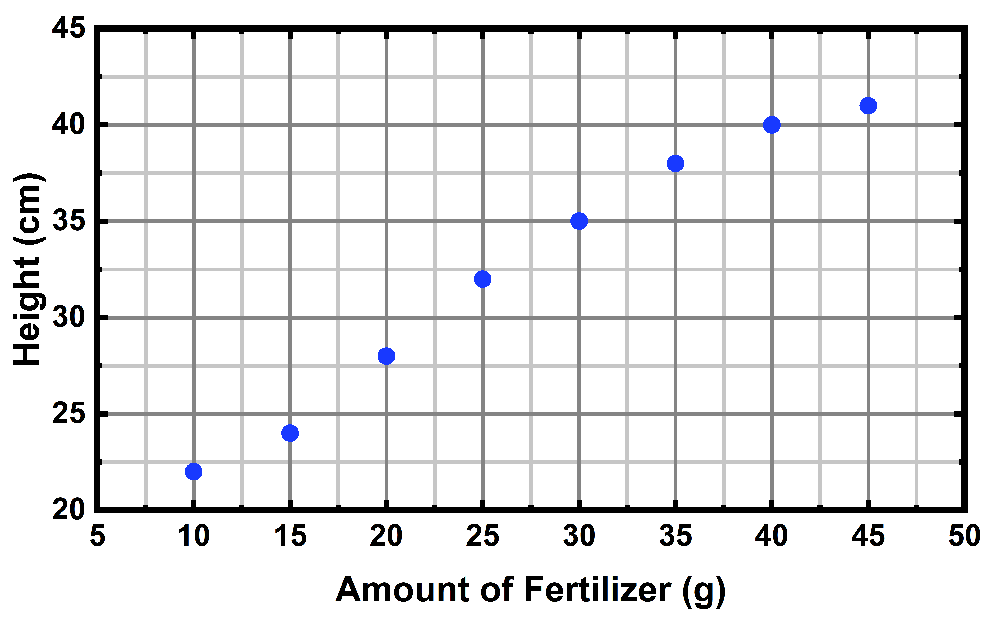
A botanist records the amount of fertilizer in grams used and the resulting height in centimeters of tomato plants after two months. The data and the corresponding scatterplot are as follows:

Calculate the value of the linear correlation coefficient $r$ and determine the critical values of $r$ at a significance level of $\alpha =0.05$. Is there enough evidence to support a claim that there is a linear correlation between the amount of fertilizer and plant height?

On a scatterplot, data points are tightly clustered around a line that slopes upward. What does this suggest about the correlation coefficient?