Which confidence level results in the widest confidence interval, assuming all other factors are constant?

A biologist records the weights in grams of two species of birds.

Species X$:15.2,15.5,15.1,15.3,15.4$

Species Y$:14.8,15.0,15.2,14.9,15.1$

Construct a $95$ percent confidence interval estimate for the variance of each species' weights. Is there evidence of a difference in variation between the two species?

A sample yields a confidence interval of (40, 52). What is the margin of error if the point estimate is 46?

If a confidence interval for a population mean is (12, 20) and the point estimate is 16, what is the margin of error?

For a 90% confidence interval, what area under the normal curve corresponds to one tail (alpha/2)?

A quality control engineer collected a simple random sample of 10 bolts produced in a batch to assess their lengths (in millimeters). The sample has the following statistics:

Sample mean $\left(\bar{x}\right)=24.07\text{ mm}$

Margin of error (ME) for a $90\%$ confidence interval $=0.11\text{ mm}$

Construct the $90\%$ confidence interval for the true mean length of bolts produced in the first batch using the given statistics. Another confidence interval for a sample of bolts from a second batch is reported as $(23.95\text{ mm},24.25\text{ mm})$. How does the result compare to the confidence interval of the second batch? Explain possible reasons for differences in their widths.

A group of $50$ volunteers participated in a mindfulness program. After $8$ weeks, their mean reduction in stress score was $4.6$ points, with a sample standard deviation of $5.3$ points. Construct a $99\%$ confidence interval estimate of the standard deviation of the reduction in stress scores for all such participants.

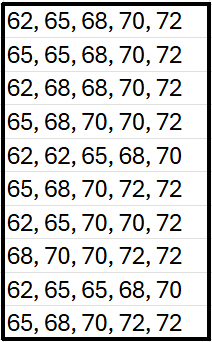
A study aims to estimate the variability in weights (in kilograms) of competitive cyclists. The following weights are recorded from a sample of $5$ cyclists: $62,65,68,70,72$. Ten bootstrap samples are provided below:

Use the $10$ bootstrap samples to construct an $80\%$ confidence interval estimate of the population standard deviation $\sigma$.

Researchers measured the simple reaction times (milliseconds) of a random sample of drivers and cyclists under identical conditions. From these samples, they computed a $95\%$ confidence interval for the difference in population mean reaction times (drivers minus cyclists) as:

What does this confidence interval suggest about whether the mean reaction time of drivers equals the mean reaction time of cyclists?

For a bootstrap percentile confidence interval at the $90\%$ level, which percentiles of the bootstrap distribution form the interval endpoints?