Area functions for linear functions Consider the following functions ƒ and real numbers a (see figure).
(b) Verify that A'(𝓍) = ƒ(𝓍).

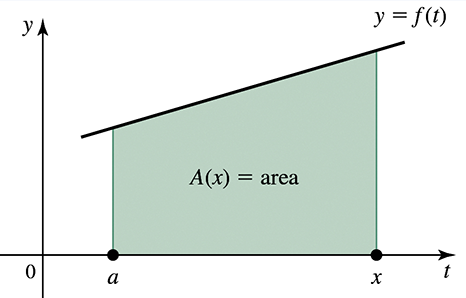
ƒ(t) = 3t + 1 , a = 2

Verified step by step guidance

Step 1: Understand the problem. The goal is to verify that the derivative of the area function A(x) with respect to x is equal to the given function f(x). The area function A(x) represents the area under the curve y = f(t) from t = a to t = x.

Step 2: Recall the Fundamental Theorem of Calculus. It states that if A(x) is defined as the integral of f(t) from a to x, then the derivative of A(x) with respect to x is equal to f(x). Mathematically, this is expressed as:

d^{d x} A (x) = f (x)

Step 3: Define the area function A(x). Using the given function f(t) = 3t + 1 and the lower limit a = 2, the area function is:

A (x) = \int_{a}^{x} (3 t + 1) d t

Step 4: Differentiate A(x) with respect to x. By the Fundamental Theorem of Calculus, the derivative of the integral with respect to its upper limit x is simply the integrand evaluated at x. Therefore,

d^{d x} A (x) = f (x) = 3 x + 1

Step 5: Verify the result. The derivative of A(x) matches the given function f(x) = 3x + 1, confirming that A'(x) = f(x). This completes the verification.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Area Function

An area function, denoted as A(x), represents the accumulated area under a curve from a fixed point 'a' to a variable point 'x'. In this context, it quantifies the area between the x-axis and the function f(t) = 3t + 1 over the interval [a, x]. Understanding this concept is crucial for analyzing how the area changes as 'x' varies.

Fundamental Theorem of Calculus

The Fundamental Theorem of Calculus links differentiation and integration, stating that if A(x) is the area function defined as the integral of f(t) from a to x, then the derivative A'(x) equals f(x). This theorem is essential for verifying the relationship between the area function and the original function, as required in the question.

Linear Functions

A linear function is a polynomial function of degree one, typically expressed in the form f(t) = mt + b, where m is the slope and b is the y-intercept. In this case, f(t) = 3t + 1 is a linear function with a slope of 3, indicating a constant rate of change. Understanding linear functions is vital for interpreting the graph and calculating the area under the curve.

Watch next

Master Fundamental Theorem of Calculus Part 1 with a bite sized video explanation from Patrick

Start learning