1. Give some examples of analytical methods for evaluating integrals.
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 34m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
7. Antiderivatives & Indefinite Integrals
Indefinite Integrals
Problem 8.7.31
Textbook Question
7–40. Table look-up integrals Use a table of integrals to evaluate the following indefinite integrals. Some of the integrals require preliminary work, such as completing the square or changing variables, before they can be found in a table.
31. ∫ √(x² - 8x) dx, x > 8
 Verified step by step guidance
Verified step by step guidance1
Rewrite the expression inside the square root to make it easier to work with. Complete the square for the quadratic expression x² - 8x. Completing the square involves rewriting x² - 8x as (x - 4)² - 16.
Substitute the completed square form into the integral: ∫ √((x - 4)² - 16) dx.
Recognize that this integral resembles a standard form found in a table of integrals, specifically one involving √(u² - a²). To match the table form, let u = x - 4 and du = dx.
Rewrite the integral in terms of u: ∫ √(u² - 16) du. Now the integral is in a standard form that can be evaluated using a table of integrals.
Use the appropriate formula from the table of integrals for ∫ √(u² - a²) du, where a² = 16. Substitute back u = x - 4 into the result to express the solution in terms of x.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Completing the Square
Completing the square is a technique used to transform a quadratic expression into a perfect square trinomial. This method is essential for simplifying integrals involving quadratic terms, as it allows for easier integration by rewriting the expression in a more manageable form. For example, the expression x² - 8x can be rewritten as (x - 4)² - 16, facilitating the integration process.
Recommended video:
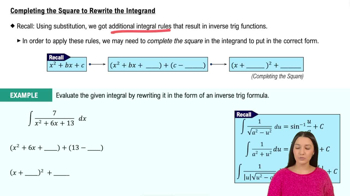
Completing the Square to Rewrite the Integrand
Indefinite Integrals
Indefinite integrals represent a family of functions whose derivative gives the integrand. They are expressed without limits and include a constant of integration, typically denoted as 'C'. Understanding how to evaluate indefinite integrals using techniques such as substitution or reference to integral tables is crucial for solving problems in calculus, including those that require preliminary transformations.
Recommended video:

Introduction to Indefinite Integrals
Integral Tables
Integral tables are collections of standard integrals that provide quick references for evaluating common integrals without performing the integration from first principles. They are particularly useful for complex functions or those that require specific techniques, such as trigonometric or exponential substitutions. Familiarity with these tables can significantly expedite the process of solving integrals, especially when combined with preliminary algebraic manipulations.
Recommended video:

Tabular Integration by Parts

 5:04m
5:04mWatch next
Master Introduction to Indefinite Integrals with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
30
views
