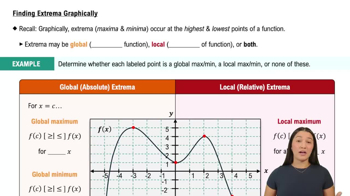
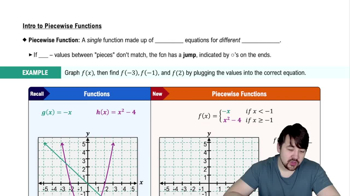
Finding Extrema from Graphs
In Exercises 1–6, determine from the graph whether the function has any absolute extreme values on [a, b]. Then explain how your answer is consistent with Theorem 1.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: