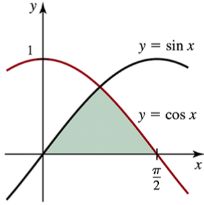
Area functions for the same linear function Let ƒ(t) = 2t ― 2 and consider the two area functions A (𝓍) = ∫₁ˣ ƒ(t) dt and F(𝓍) = ∫₄ˣ ƒ(t) dt .
(a) Evaluate A (2) and A (3). Then use geometry to find an expression for A (𝓍) , for 𝓍 ≥ 1 .
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 5:23m
5:23mMaster Finding Area Between Curves on a Given Interval with a bite sized video explanation from Patrick
Start learning