Multiple Choice
Graph
84
views
1
rank
16. Parametric Equations & Polar Coordinates
Polar Coordinates
1:11 minutesProblem 12.2.50
Textbook Question
49–52. Cartesian-to-polar coordinates Convert the following equations to polar coordinates.
y = 3
Verified step by step guidance1
Recall the relationships between Cartesian coordinates \((x, y)\) and polar coordinates \((r, \theta)\): \(x = r \cos{\theta}\) and \(y = r \sin{\theta}\).
Given the equation \(y = 3\), substitute \(y\) with its polar form: \(r \sin{\theta} = 3\).
Isolate \(r\) to express it in terms of \(\theta\): \(r = \frac{3}{\sin{\theta}}\).
Note the domain restrictions where \(\sin{\theta} \neq 0\) to avoid division by zero.
The polar form of the equation \(y = 3\) is therefore \(r = \frac{3}{\sin{\theta}}\).
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mKey Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Polar Coordinates System
Polar coordinates represent points in the plane using a radius and an angle, denoted as (r, θ), where r is the distance from the origin and θ is the angle measured from the positive x-axis. This system is useful for describing curves that are difficult to express in Cartesian coordinates.
Recommended video:
05:32
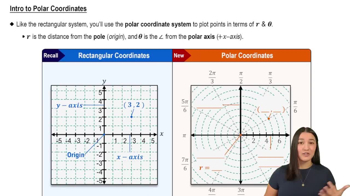
Intro to Polar Coordinates
Conversion Formulas Between Cartesian and Polar Coordinates
To convert from Cartesian (x, y) to polar (r, θ), use r = √(x² + y²) and θ = arctan(y/x). Conversely, x = r cos(θ) and y = r sin(θ). These formulas allow rewriting equations from one coordinate system to the other.
Recommended video:
05:32Intro to Polar Coordinates
Expressing Cartesian Equations in Polar Form
To convert a Cartesian equation like y = 3 into polar form, substitute y with r sin(θ). This transforms the equation into r sin(θ) = 3, which can then be analyzed or manipulated using polar coordinates.
Recommended video:
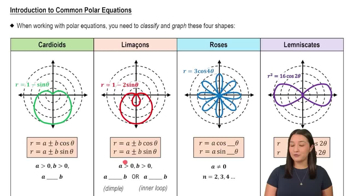
3:47Introduction to Common Polar Equations
5:32mWatch next
Master Intro to Polar Coordinates with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice