Finding Formulas for Functions
A point P in the first quadrant lies on the graph of the function f(x) = √x. Express the coordinates of P as functions of the slope of the line joining P to the origin.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: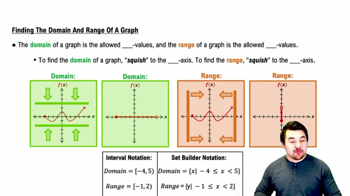


 1:36m
1:36mMaster Introduction to Calculus Channel with a bite sized video explanation from Patrick
Start learning