Here are the essential concepts you must grasp in order to answer the question correctly.
Definite Integrals
A definite integral represents the signed area under a curve between two specified limits. It is denoted as ∫ from a to b of f(x) dx, where 'a' and 'b' are the lower and upper limits, respectively. The result of a definite integral is a numerical value that quantifies the accumulation of the function's values over the interval [a, b].
Recommended video:
Definition of the Definite Integral
Integration Techniques
Integration techniques are methods used to evaluate integrals that may not be solvable by basic antiderivatives. Common techniques include substitution, integration by parts, and partial fraction decomposition. For the integral in the question, recognizing the form of the denominator can guide the choice of technique to simplify the expression before integrating.
Recommended video:
Integration by Parts for Definite Integrals
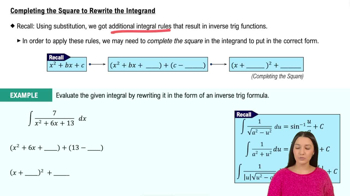
Polynomial Division and Completing the Square
Polynomial division and completing the square are algebraic techniques that can simplify integrals involving polynomials. Completing the square transforms a quadratic expression into a perfect square form, which can facilitate integration. In the given integral, rewriting the denominator x² + 4x + 8 in a completed square form can help in applying substitution or recognizing a standard integral form.
Recommended video:
Completing the Square to Rewrite the Integrand
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 8:38m
8:38m