Planetary orbits The planets orbit the Sun in...

Question

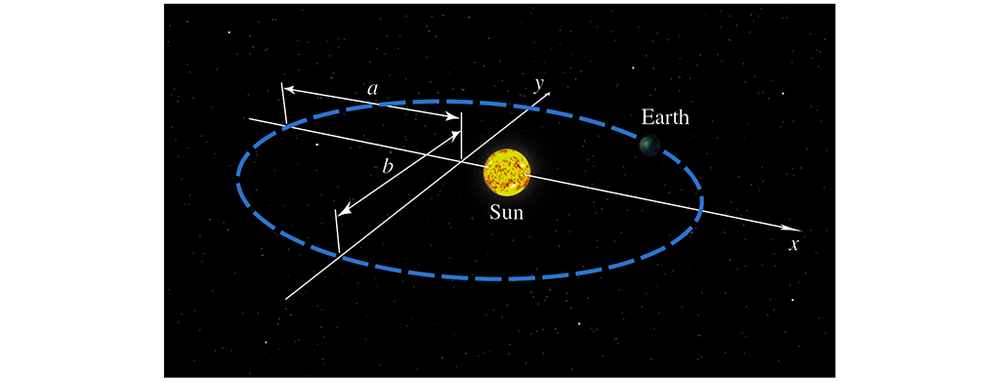
Planetary orbits The planets orbit the Sun in elliptical orbits with the Sun at one focus (see Section 12.4 for more on ellipses). The equation of an ellipse whose dimensions are 2a in the 𝓍-direction and 2b in the y-direction is (𝓍²/a²) + (y² /b²) = 1.

(a) Let d² denote the square of the distance from a planet to the center of the ellipse at (0, 0). Integrate over the interval [ ―a, a] to show that the average value of d² is (a² + 2b²) /3 .

Diagram of an elliptical orbit with the Sun at one focus, labeled axes, and the Earth positioned along the orbit.

Accepted Answer

Hi, everyone, let's take a look at this practice problem. This problem says let an ellipse be defined by X2 divided by M2 plus Y2 divided by N2 equal to 1. For a point X Y on the ellipse, let S2 be the square of its distance to the center. Find the average value of S2 as X runs from minus M to M. Now, we need to find the average value of Squad, and we're told that S2 is the square of the distance from a point on the ellipse to its center. So that means that S2 is going to be equal to X2 plus Y2. Now, we ultimately want to have S2 in terms of a single variable. So we're going to use our equation for our lips to write our variable Y in terms of X. So if we take our equation for ellipse, which is X2 divided by M2 plus Y2 divided by n2 equal to 1, and we'll need to solve this for Y2. So the first step is to subtract X2 divided by M2 from both sides of the equation. So doing so, we'll get Y2 divided by N2 is equal to 1 minus X2 divided by m2. And to solve for Y2, we now just need to multiply both sides of the equation by N2. In doing so, we will have Y2 as equal to n2, multiplied by the quantity of 1 minus X2 divided by M2n quantity. So when I'll substitute this back into our expression for Squad. So Squad is going to be equal to X2. Plus n2 multiplied by the quantity of 1 minus X2 divided by m2 in quantity. And so collecting like terms we see that this is going to be equal to the quantity of 1 minus n2 divided by m2n quantity multiplied by X2 plus n2d. So now we need to find the average value of Squad. And so we're gonna call that quantity Squared average. And this is going to be equal to, and here we call how you find the average value of a function. So we'll have 1 divided by the interval. We'll have 1 divided by, and here we're looking at the interval as X runs from minus M to M. So we'll have on the denominator here, the quantity of M minus minus M and quantity, and this gets multiplied by the interval from minus M. Tom of Squad, which is going to be the quantity of quantity of 1 minus N2 divided by M2, and quantity X2. Plus N2, in quantity DX as we're integrating with respect to X. Now, if we look at our integrate here, we're going to be integrating an even function. So that means that we can use the symmetry of an even function to rewrite the limits of our integration to go from 0 to M, but we'd have to multiply the entire integral by 2. That's what we're going to do. That means that S2 average is going to be equal to, and here we'll simplify the coefficient out front, so we'll have 1 divided by the quantity of 2 M. Then we need to multiply our integral by 2, so we'll need to multiply that by 2. And we'll have the integral going from 0 to M, of the quantity of quantity of 1 minus N2d divided by M2, and quantity multiplied by X2 plus N2. In quantity, DX. So now we just need to integrate each of those terms inside our integra. So in doing so, this is going to be equal to. Here, we'll simplify the coefficient out front again, and we'll just have 1 divided by M multiplied by the quantity, and here we'll have the quantity of 1 minus n2 divided by m2 in quantity, and that gets multiplied by the integral of X2d with respect to X. And when we integrate X2 with respect to x, recall that we get X cubed divided by 3. Then we'll have plus. And here in the next term, we're just integrating a constant and squared. So when we integrate a constant, With respect to X, we get that constant back of N2d multiplied by X. And then we'll have to end that quantity, and this whole quantity is evaluated from 0 to M. And now substituting in our limits of integration, we see that this is going to be equal to 1 divided by M, multiplied by the quantity of the quantity of 1 minus N2d divided by M2d and quantity multiplied by M cubed divided by 3. Plus N2 multiplied by M minus the quantity of the quantity of 1 minus N2 divided by M2d and quantity multiplied by. 0 cubed divided by 3. Plus n2 multiplied by 0 in quantity. And so simplifying this expression, we see that this is going to be equal to 1 divided by M, multiplied by the quantity, and here we'll go ahead and multiply everything out. So we'll have M cubed divided by 3. Minus the next term. We have And squared Multiplied by M divided by 3. Plus N squared multiplied by M. -0-0 in quantity. So now we can distribute our 1 divided by M out in front. In doing so, we see that S2 average is going to be equal to M2 divided by 3. Minus N2 divided by 3, plus N2. And simplifying this by collecting like terms and putting everything on a common denominator, we see that S2 average is going to be equal to the quantity of M2 plus 2 N2. Divided by 3. So this here is the answer that we're looking for for this problem. So, I hope that this explanation has been useful, and I'll see you in the next video.

Key Concepts

Elliptical Orbits

Average Value of a Function

Integration

Watch next