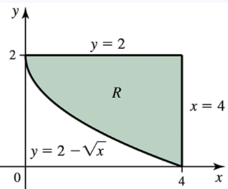
Let R be the region in the first quadrant bounded above by the curve y=2−x² and bounded below by the line y=x. Suppose the shell method is used to determine the volume of the solid generated by revolving R about the y-axis.
a. What is the radius of a cylindrical shell at a point x in [0, 2]?