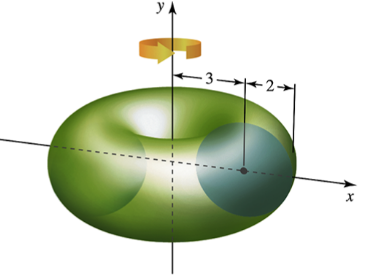
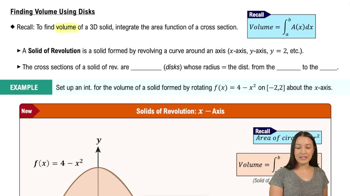
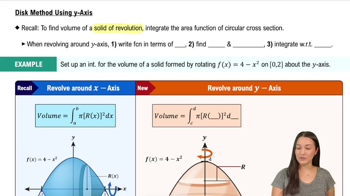
Volume of a sphere Let R be the region bounded by the upper half of the circle x²+y² = r² and the x-axis. A sphere of radius r is obtained by revolving R about the x-axis.
a. Use the shell method to verify that the volume of a sphere of radius r is 4/3 πr³.