Textbook Question
69. Comparing volumes Let R be the region bounded by y = sin x and the x-axis on the interval [0, π]. Which is greater, the volume when R is revolved about the x-axis, or the volume when R is revolved about the y-axis?
18
views
9. Graphical Applications of Integrals
Introduction to Volume & Disk Method
2:58 minutesProblem 6.R.42b
Textbook Question
Two methods The region R in the first quadrant bounded by the parabola y = 4-x² and coordinate axes is revolved about the y-axis to produce a dome-shaped solid. Find the volume of the solid in the following ways:
b. Apply the shell method and integrate with respect to x.
Verified step by step guidance1
Identify the region R bounded by the parabola \(y = 4 - x^{2}\) and the coordinate axes in the first quadrant. Since we are in the first quadrant, \(x\) ranges from 0 to the point where the parabola meets the x-axis, which is found by solving \$4 - x^{2} = 0$.
Set up the shell method formula for volume when revolving around the y-axis. The volume \(V\) is given by the integral \(V = \int_{a}^{b} 2\pi \cdot (\text{radius}) \cdot (\text{height}) \, dx\), where the radius is the distance from the y-axis (which is \(x\)) and the height is the function value \(y = 4 - x^{2}\).
Determine the limits of integration \(a\) and \(b\). Since the region is bounded between \(x=0\) and the x-intercept of the parabola, \(b\) is the positive root of \$4 - x^{2} = 0\(, which is \)x=2$.
Write the integral explicitly: \(V = \int_{0}^{2} 2\pi x (4 - x^{2}) \, dx\). This integral represents the volume of the solid formed by revolving the region around the y-axis using the shell method.
To find the volume, expand the integrand and integrate term-by-term with respect to \(x\) over the interval \([0, 2]\). After integrating, evaluate the definite integral at the limits to express the volume.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mKey Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Shell Method for Volume
The shell method calculates the volume of a solid of revolution by summing cylindrical shells. Each shell's volume is approximated by its circumference times height times thickness. When revolving around the y-axis, shells are vertical slices parallel to the axis, integrated with respect to x.
Recommended video:
04:48
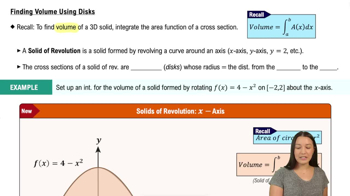
Finding Volume Using Disks
Setting up the Integral with Respect to x
To use the shell method with respect to x, identify the radius as the distance from the y-axis (x), the height as the function value y = 4 - x², and the thickness as dx. The integral bounds correspond to the x-values where the region exists, here from 0 to 2.
Recommended video:
03:39Integrals of Natural Exponential Functions (e^x)
Region Bounded by the Parabola and Axes
The region R lies in the first quadrant bounded by y = 4 - x², the x-axis, and the y-axis. Understanding these boundaries helps determine the limits of integration and the shape of the solid formed when revolved around the y-axis.
Recommended video:
7:42Properties of Parabolas
5:38mWatch next
Master Introduction to Cross Sections with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice