A cone is formed from a circular piece of material of radius 1 meter by removing a section of angle θ and then joining the two straight edges. Determine the largest possible volume for the cone.
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 34m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
5. Graphical Applications of Derivatives
Applied Optimization
Problem 4.5.41
Textbook Question
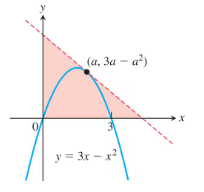
41. Among all triangles in the first quadrant formed by the x-axis, the y-axis, and tangent lines to the graph of y=3x-x^2, what is the smallest possible area?
 Verified step by step guidance
Verified step by step guidance1
Identify the function y = 3x - x^2 and note that the problem involves finding the area of triangles formed by tangent lines to this curve in the first quadrant.
Find the derivative of the function y = 3x - x^2 to determine the slope of the tangent line at any point (a, 3a - a^2). The derivative is dy/dx = 3 - 2x.
The equation of the tangent line at point (a, 3a - a^2) is y - (3a - a^2) = (3 - 2a)(x - a). Simplify this to find the y-intercept and x-intercept of the tangent line.
The x-intercept occurs when y = 0, and the y-intercept occurs when x = 0. Use these intercepts to determine the base and height of the triangle formed by the tangent line, the x-axis, and the y-axis.
Express the area of the triangle as a function of a, A(a) = (1/2) * base * height. Differentiate A(a) with respect to a, set the derivative equal to zero, and solve for a to find the value that minimizes the area.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Tangent Line to a Curve
A tangent line to a curve at a given point is a straight line that just touches the curve at that point. It has the same slope as the curve at the point of tangency. For the function y = 3x - x^2, the slope of the tangent line at any point (a, 3a - a^2) is given by the derivative, which is 3 - 2a.
Recommended video:
Slopes of Tangent Lines
Area of a Triangle
The area of a triangle can be calculated using the formula: Area = 0.5 * base * height. In this context, the triangle is formed by the x-axis, y-axis, and the tangent line. The base and height are determined by the x and y intercepts of the tangent line, which can be found using the point-slope form of the line equation.
Recommended video:
Finding Area When Bounds Are Not Given
Optimization in Calculus
Optimization involves finding the maximum or minimum value of a function. In this problem, we need to minimize the area of the triangle. This requires setting up an equation for the area in terms of a single variable, differentiating it, and finding critical points to determine the minimum area using the first or second derivative test.
Recommended video:

Intro to Applied Optimization: Maximizing Area

 1:13m
1:13mWatch next
Master Intro to Applied Optimization: Maximizing Area with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
119
views
