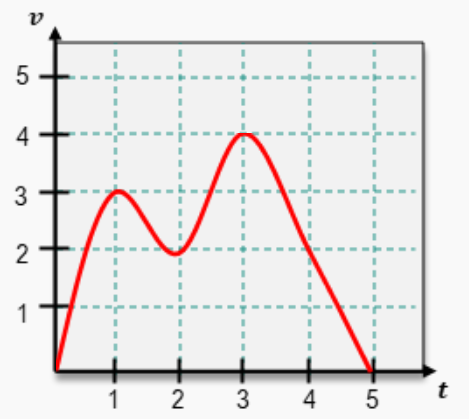
Terminal velocity Refer to Exercises 95 and 96.
d. How tall must a cliff be so that the BASE jumper (m = 75 kg and k = 0.2) reaches 95% of terminal velocity? Assume the jumper needs at least 300 m at the end of free fall to deploy the chute and land safely.