How do you obtain the graph of from the graph of ?
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
0. Functions
Transformations
Problem 14e
Textbook Question
Use the graph of f in the figure to plot the following functions.
<IMAGE>
y=f(x−1)+2
 Verified step by step guidance
Verified step by step guidance1
Identify the transformation components in the function y = f(x-1) + 2. The function involves a horizontal shift and a vertical shift.
Recognize that the expression (x-1) indicates a horizontal shift. Specifically, f(x-1) represents a shift of the graph of f(x) to the right by 1 unit.
Understand that the '+2' outside the function indicates a vertical shift. This means that after shifting the graph to the right, you will move it up by 2 units.
Start by taking each point on the original graph of f(x) and apply the horizontal shift. Move each point 1 unit to the right.
After applying the horizontal shift, apply the vertical shift by moving each of the new points 2 units up. Plot these new points to obtain the graph of y = f(x-1) + 2.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Function Transformation
Function transformation refers to the changes made to the graph of a function through operations such as shifting, stretching, or reflecting. In the given equation, y = f(x - 1) + 2, the function f is shifted to the right by 1 unit and then raised vertically by 2 units. Understanding these transformations is crucial for accurately plotting the new function based on the original graph.
Recommended video:
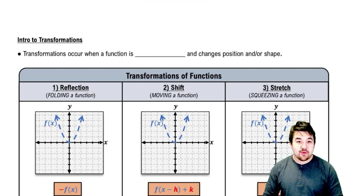
Intro to Transformations
Horizontal Shift
A horizontal shift occurs when a function is moved left or right along the x-axis. In the expression f(x - 1), the subtraction of 1 indicates a shift to the right by 1 unit. This concept is essential for determining how the input values of the function are altered, affecting the overall position of the graph.
Recommended video:
Horizontal Parabolas
Vertical Shift
A vertical shift involves moving a function up or down along the y-axis. In the equation y = f(x - 1) + 2, the addition of 2 results in a vertical shift upwards by 2 units. This concept helps in understanding how the output values of the function are adjusted, which is necessary for accurately plotting the transformed function.
Recommended video:
Foci and Vertices of an Ellipse

 5:25m
5:25mWatch next
Master Intro to Transformations with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
222
views
