Rationalize each denominator. Assume all variables represent nonnegative numbers and that no denominators are 0.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 4b
Textbook Question
Match the rational exponent expression in Column I with the equivalent radical expression in Column II. Assume that x is not 0. -3x-1/3
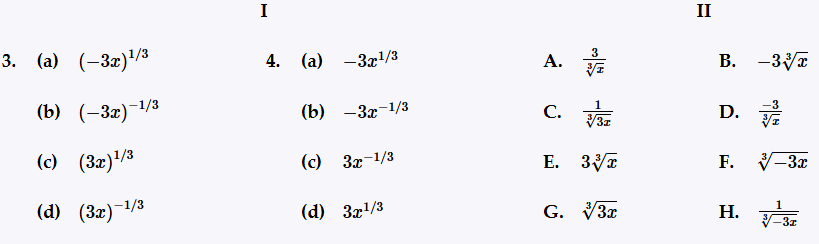
 Verified step by step guidance
Verified step by step guidance1
Identify the given expression: \(-3x^{-\frac{1}{3}}\).
Recall that a rational exponent \(x^{\frac{m}{n}}\) can be rewritten as a radical: \(x^{\frac{m}{n}} = \sqrt[n]{x^m}\).
Apply this to the term \(x^{-\frac{1}{3}}\): rewrite it as \(\left(\sqrt[3]{x}\right)^{-1}\), which is the reciprocal of the cube root of \(x\).
Since the exponent is negative, rewrite \(x^{-\frac{1}{3}}\) as \(\frac{1}{x^{\frac{1}{3}}} = \frac{1}{\sqrt[3]{x}}\).
Combine the coefficient \(-3\) with the radical expression to get the equivalent radical form: \(-3 \cdot \frac{1}{\sqrt[3]{x}} = \frac{-3}{\sqrt[3]{x}}\).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Exponents
Rational exponents express roots and powers simultaneously, where the numerator indicates the power and the denominator indicates the root. For example, x^(m/n) means the nth root of x raised to the mth power, or (√[n]{x})^m.
Recommended video:
Guided course

Rational Exponents
Negative Exponents
A negative exponent indicates the reciprocal of the base raised to the corresponding positive exponent. For instance, x^(-a) equals 1 divided by x^a, which flips the base to the denominator.
Recommended video:
Guided course

Zero and Negative Rules
Converting Rational Exponents to Radical Expressions
To convert a rational exponent to a radical expression, rewrite x^(m/n) as the nth root of x raised to the mth power: x^(m/n) = √[n]{x^m}. This helps in matching expressions involving radicals and rational exponents.
Recommended video:
Guided course

Rational Exponents
Related Videos
Related Practice
Textbook Question
865
views


