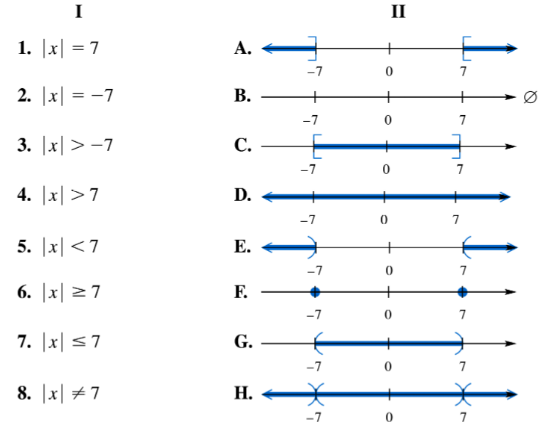
Match the inequality in each exercise in Column I with its equivalent interval notation in Column II. 6≤x
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Linear Inequalities
Problem 8
Textbook Question
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | ≠ 7
 Verified step by step guidance
Verified step by step guidance1
Understand the inequality \( |x| \neq 7 \) means the absolute value of \( x \) is not equal to 7. This excludes the points where \( x = 7 \) and \( x = -7 \).
Recall that \( |x| = 7 \) corresponds to the two points \( x = 7 \) and \( x = -7 \) on the number line.
Since the inequality is \( |x| \neq 7 \), the solution set includes all real numbers except \( x = 7 \) and \( x = -7 \).
On the graph, this will be represented by the entire number line with open circles (or holes) at \( x = 7 \) and \( x = -7 \), indicating these points are not included.
Match this description to the graph in Column II that shows all points except \( x = 7 \) and \( x = -7 \) excluded.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Absolute Value
The absolute value of a number represents its distance from zero on the number line, always as a non-negative value. For example, |x| = 7 means x is either 7 or -7, since both are 7 units from zero.
Recommended video:

Parabolas as Conic Sections Example 1
Inequalities Involving Absolute Value
An inequality like |x| ≠ 7 means x cannot be exactly 7 or -7, but can be any other real number. Understanding how to interpret and graph such inequalities is essential for matching them to their solution sets.
Recommended video:

Linear Inequalities
Graphing Solution Sets on the Number Line
Graphing solution sets involves representing all values that satisfy an equation or inequality on a number line. For |x| ≠ 7, the graph excludes points at 7 and -7, showing all other points shaded or included.
Recommended video:
Guided course

Graphing Lines in Slope-Intercept Form
Related Videos
Related Practice
Textbook Question
608
views


