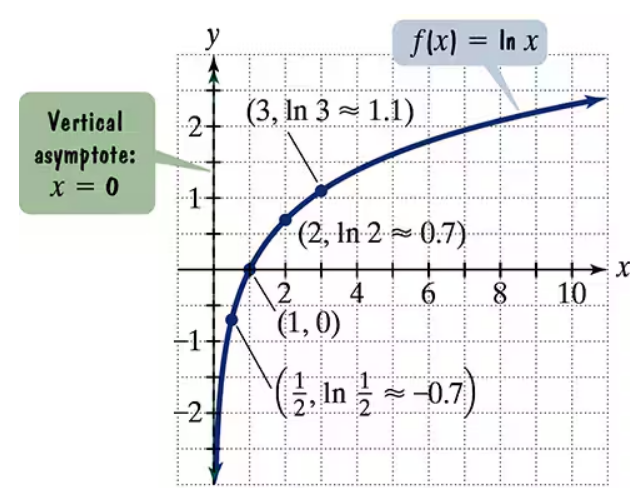
The figure shows the graph of f(x) = ln x. In Exercises 65–74, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range.
h(x) = ln (2x)

The natural logarithm function, denoted as f(x) = ln(x), is the inverse of the exponential function e^x. It is defined for positive real numbers and has a vertical asymptote at x = 0. The function is increasing and passes through the point (1, 0), where ln(1) = 0. Understanding its properties is crucial for analyzing transformations.

Transformations of functions involve shifting, stretching, compressing, or reflecting the graph of a function. For example, the function h(x) = ln(2x) represents a horizontal compression by a factor of 2. Recognizing how these transformations affect the graph's shape and position is essential for accurately graphing the transformed function.

Asymptotes are lines that a graph approaches but never touches. For the natural logarithm function, the vertical asymptote is at x = 0, indicating that as x approaches 0 from the right, f(x) approaches negative infinity. Identifying asymptotes helps in determining the behavior of the function and its domain and range.