In the following exercises, (a) find the center-radius form of the equation of each circle described, and (b) graph it. center (0, 4), radius 4
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 25
Textbook Question
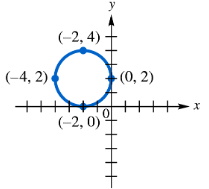
Use each graph to determine an equation of the circle in (a) center-radius form and (b) general form.
 Verified step by step guidance
Verified step by step guidance1
Identify the center \((h, k)\) of the circle from the graph. This is the point where the circle is centered.
Determine the radius \(r\) of the circle by measuring the distance from the center to any point on the circle.
Write the equation of the circle in center-radius form using the formula:
\[ (x - h)^2 + (y - k)^2 = r^2 \]
Expand the squared terms in the center-radius form to convert it into the general form. This involves expanding \((x - h)^2\) and \((y - k)^2\).
Simplify the expanded expression and rearrange all terms to one side to write the equation in general form:
\[ x^2 + y^2 + Dx + Ey + F = 0 \] where \(D\), \(E\), and \(F\) are constants derived from the expansion.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Equation of a Circle in Center-Radius Form
The center-radius form of a circle's equation is (x - h)² + (y - k)² = r², where (h, k) is the center and r is the radius. This form directly shows the circle's center coordinates and radius, making it easy to write the equation when these values are known from the graph.
Recommended video:

Circles in Standard Form
Converting to General Form of a Circle
The general form of a circle's equation is x² + y² + Dx + Ey + F = 0. It is obtained by expanding the center-radius form and simplifying. Understanding how to expand and rearrange terms is essential to rewrite the equation in this standard polynomial form.
Recommended video:
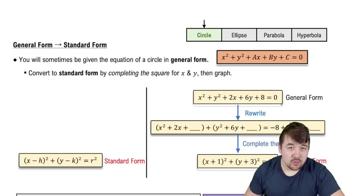
Circles in General Form
Interpreting Graphs to Identify Circle Parameters
Analyzing a graph of a circle involves identifying the center point and measuring the radius, which is the distance from the center to any point on the circle. Accurate reading of these values from the graph is crucial for writing the correct equation in both forms.
Recommended video:

Circles in Standard Form

 5:2m
5:2mWatch next
Master Relations and Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
568
views
