Determine whether each relation defines y as a function of x. Give the domain and range. y=√(7-2x)
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 97
Textbook Question
For each function graphed, give the minimum and maximum values of ƒ(x) and the x-values at which they occur.
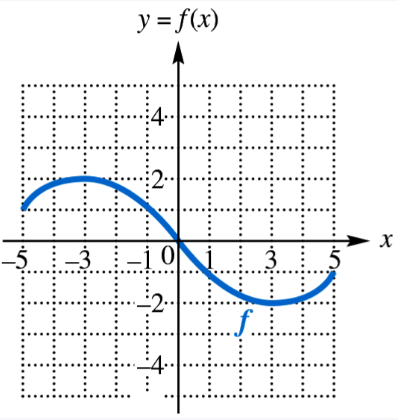
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the maximum value of the function by locating the highest point on the graph. This is where the function reaches its peak.
Step 2: Note the y-coordinate of this highest point, which represents the maximum value of ƒ(x), and the corresponding x-coordinate where this maximum occurs.
Step 3: Identify the minimum value of the function by locating the lowest point on the graph. This is where the function reaches its lowest value.
Step 4: Note the y-coordinate of this lowest point, which represents the minimum value of ƒ(x), and the corresponding x-coordinate where this minimum occurs.
Step 5: Summarize the results by stating the minimum and maximum values of ƒ(x) along with their respective x-values.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Maximum and Minimum Values of a Function
Maximum and minimum values of a function are the highest and lowest points on its graph, respectively. A maximum value is where the function reaches a peak, and a minimum value is where it reaches a trough. These values can be local (relative) or absolute (global) within a given domain.
Recommended video:

Maximum Turning Points of a Polynomial Function
Reading and Interpreting Graphs
Understanding how to read graphs involves identifying key points such as peaks, valleys, and intercepts. The x-values at these points correspond to where the function attains its maximum or minimum values. Accurate interpretation helps in extracting meaningful information about the function's behavior.
Recommended video:
Guided course

Graphs and Coordinates - Example
Function Notation and Evaluation
Function notation, written as ƒ(x), represents the output of a function for a given input x. Evaluating the function at specific x-values helps determine the corresponding y-values, which are essential for identifying minimum and maximum points on the graph.
Recommended video:

Evaluating Composed Functions

 5:2m
5:2mWatch next
Master Relations and Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
538
views
