Textbook Question
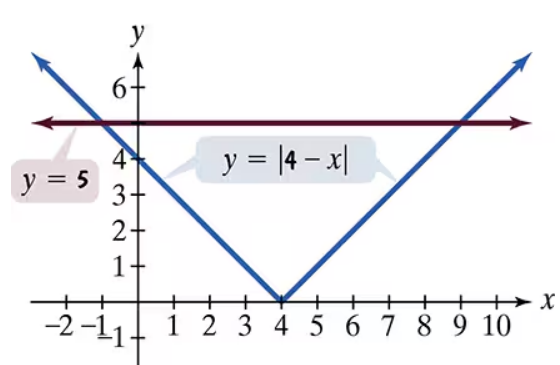
Use the method described in Exercises 83–86, if applicable, and properties ofabsolute value to solve each equation or inequality. (Hint: Exercises 99 and 100 canbe solved by inspection.) | x^4 + 2x^2 + 1 | < 0
525
views
1. Equations & Inequalities
Linear Inequalities
3:08 minutesProblem 104
Textbook Question
In Exercises 103–104, use the graph of y = |4 - x| to solve each inequality. 
|4 - x| ≥ 5
Verified step by step guidance1
Step 1: Understand the inequality |4 - x| ≥ 5. This means we are looking for values of x where the absolute value of (4 - x) is greater than or equal to 5.
Step 2: Recall the definition of absolute value. For |4 - x| ≥ 5, this splits into two cases: (1) 4 - x ≥ 5, and (2) 4 - x ≤ -5.
Step 3: Solve the first case, 4 - x ≥ 5. Subtract 4 from both sides to isolate -x, resulting in -x ≥ 1. Then divide by -1 (remember to reverse the inequality sign), giving x ≤ -1.
Step 4: Solve the second case, 4 - x ≤ -5. Subtract 4 from both sides to isolate -x, resulting in -x ≤ -9. Then divide by -1 (remember to reverse the inequality sign), giving x ≥ 9.
Step 5: Combine the solutions from both cases. The inequality |4 - x| ≥ 5 is satisfied for x ≤ -1 or x ≥ 9. These intervals can be written as (-∞, -1] ∪ [9, ∞).
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Absolute Value Function
The absolute value function, denoted as |x|, represents the distance of x from zero on the number line, always yielding a non-negative result. In the context of the inequality |4 - x| ≥ 5, it indicates that the expression 4 - x can be either greater than or equal to 5 or less than or equal to -5, leading to two separate cases to solve.
Recommended video:
4:56
Function Composition
Inequalities
Inequalities express a relationship where one side is not necessarily equal to the other, using symbols like ≥, ≤, >, or <. In this case, the inequality |4 - x| ≥ 5 requires finding the values of x that satisfy this condition, which involves determining the intervals where the absolute value expression meets or exceeds 5.
Recommended video:
06:07Linear Inequalities
Graphing Absolute Value Functions
Graphing absolute value functions involves plotting the V-shaped graph that reflects the behavior of the function. The vertex of the graph represents the minimum value, and the arms extend infinitely in both directions. Understanding the graph of y = |4 - x| helps visualize the solutions to the inequality by identifying the x-values where the graph is above or equal to the horizontal line y = 5.
Recommended video:
05:25Graphing Polynomial Functions
Related Videos
Related Practice