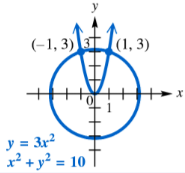
Answer each of the following. When appropriate, fill in the blank to correctly complete the sentence. If we want to solve the following nonlinear system by substitution and we decide to solve equation (2) for y, what will be the resulting equation when the substitution is made into equation (1)?
x2 + y = 2 (1)
x - y = 0 (2)