Table of contents

0. Review of Algebra4h 18m
1. Equations & Inequalities3h 18m
2. Graphs of Equations43m
3. Functions2h 17m
4. Polynomial Functions1h 44m
5. Rational Functions1h 23m
6. Exponential & Logarithmic Functions2h 28m
7. Systems of Equations & Matrices4h 6m
8. Conic Sections2h 23m
9. Sequences, Series, & Induction1h 22m
10. Combinatorics & Probability1h 45m

1. Equations & Inequalities

Intro to Quadratic Equations

College Algebra

1. Equations & Inequalities

Intro to Quadratic Equations

Previous problemNext problem

1:50 minutes

Problem 111

Textbook Question

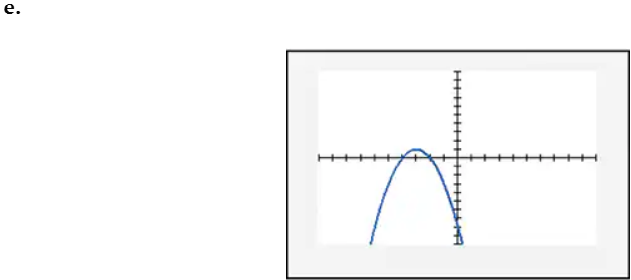
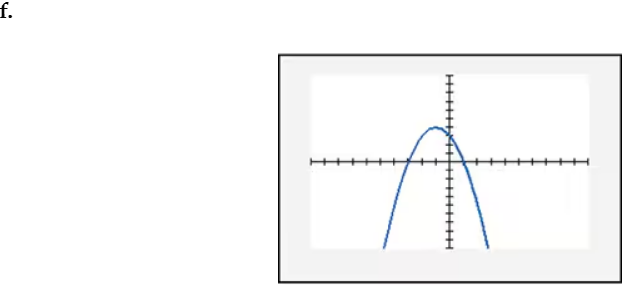
In Exercises 109–114, find the x-intercept(s) of the graph of each equation. Use the x-intercepts to match the equation with its graph. The graphs are shown in [- 10, 10, 1] by [- 10, 10, 1] viewing rectangles and labeled (a) through (f). y = - (x + 1)^2 + 4

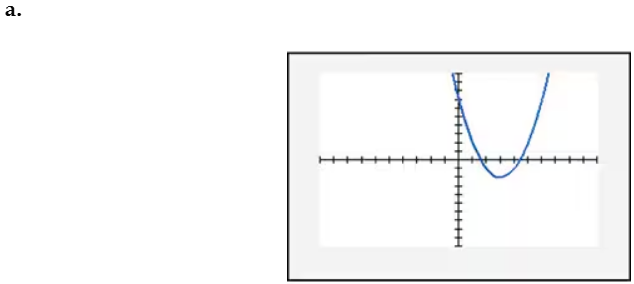
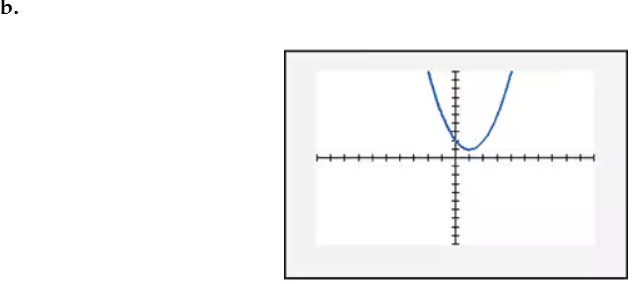
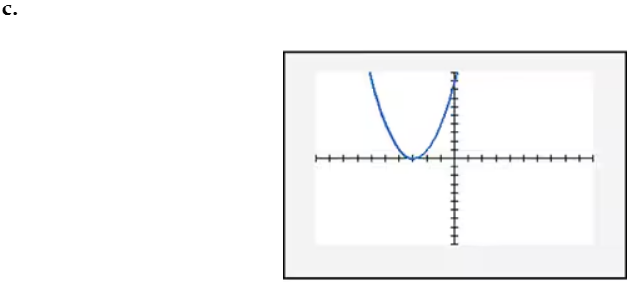
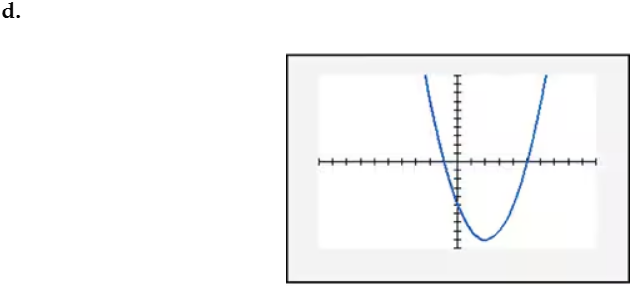
Verified step by step guidance

To find the x-intercepts of the equation \( y = - (x + 1)^2 + 4 \), set \( y = 0 \) because x-intercepts occur where the graph crosses the x-axis.

The equation becomes \( 0 = - (x + 1)^2 + 4 \).

Rearrange the equation to isolate the squared term: \( (x + 1)^2 = 4 \).

Take the square root of both sides to solve for \( x + 1 \): \( x + 1 = \pm 2 \).

Solve for \( x \) by subtracting 1 from both sides: \( x = 2 - 1 \) and \( x = -2 - 1 \), which gives the x-intercepts.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

X-Intercept

The x-intercept of a graph is the point where the graph intersects the x-axis. This occurs when the value of y is zero. To find the x-intercept, you set the equation equal to zero and solve for x. In the context of the given equation, identifying the x-intercept is crucial for understanding the graph's behavior and its relationship to the equation.

Quadratic Functions

The equation provided, y = - (x + 1)^2 + 4, is a quadratic function, which is characterized by its parabolic shape. Quadratic functions can open upwards or downwards depending on the sign of the leading coefficient. In this case, the negative sign indicates that the parabola opens downwards, affecting the location of the vertex and the x-intercepts.

Vertex Form of a Quadratic

The vertex form of a quadratic function is expressed as y = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. The given equation can be rewritten to identify its vertex, which helps in sketching the graph and understanding its maximum or minimum point. The vertex is crucial for determining the range of the function and the position of the x-intercepts.