Solve each problem. If y varies inversely as x, and y=10 when x=3, find y when x=20.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Rational Equations
Problem 19
Textbook Question
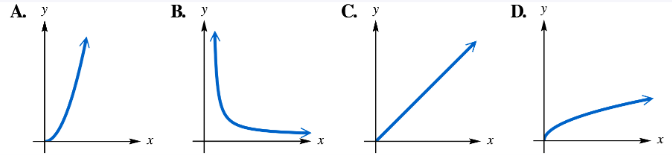
Match each statement with its corresponding graph in choices A–D. In each case, k > 0. y varies directly as the second power of x. (y=kx2)
 Verified step by step guidance
Verified step by step guidance1
Identify the type of variation described: "y varies directly as the second power of x" means the relationship can be written as \(y = kx^{2}\), where \(k > 0\).
Recognize the shape of the graph for \(y = kx^{2}\): Since \(k\) is positive and the power of \(x\) is 2, the graph is a parabola opening upwards.
Recall key features of the parabola \(y = kx^{2}\): It is symmetric about the y-axis, passes through the origin (0,0), and as \(|x|\) increases, \(y\) increases quadratically.
Compare the given graph choices A–D to these characteristics: Look for the graph that shows a U-shaped curve opening upwards, symmetric about the y-axis, and passing through the origin.
Match the statement \(y = kx^{2}\) with the graph that fits these features, confirming it represents direct variation with the second power of \(x\).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Direct Variation
Direct variation describes a relationship where one variable is equal to a constant multiplied by another variable raised to a power. In this case, y varies directly as x squared, meaning y = kx², where k is a positive constant. This implies that as x increases, y changes proportionally to the square of x.
Recommended video:

Maximum Turning Points of a Polynomial Function
Quadratic Functions and Their Graphs
A quadratic function has the form y = ax² + bx + c, and its graph is a parabola. For y = kx² with k > 0, the parabola opens upward and is symmetric about the y-axis. Understanding the shape and orientation of this graph helps in matching the equation to its correct graph.
Recommended video:

Graphs of Logarithmic Functions
Effect of the Constant k on the Graph
The constant k in y = kx² affects the steepness or width of the parabola. When k > 0, the parabola opens upward; larger values of k make the parabola narrower, while smaller values make it wider. Recognizing how k influences the graph aids in identifying the correct match among given options.
Recommended video:

Transformations of Exponential Graphs

 5:56m
5:56mWatch next
Master Introduction to Rational Equations with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
512
views
