Use vertices and asymptotes to graph each hyperbola. Locate the foci and find the equations of the asymptotes. y2/16−x2/36=1
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
8. Conic Sections
Hyperbolas NOT at the Origin
Problem 29
Textbook Question
Find the standard form of the equation of each hyperbola.
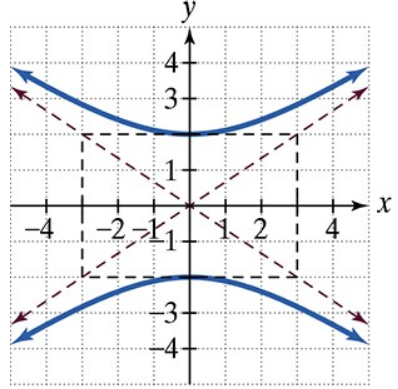
 Verified step by step guidance
Verified step by step guidance1
Identify the center of the hyperbola. From the graph, the hyperbola is centered at the origin (0, 0).
Determine the coordinates of the vertices. The vertices are given as (0, 7) and (0, -7), so the distance from the center to each vertex is 7. This means \(a = 7\).
Since the vertices lie on the y-axis, the hyperbola opens vertically. The standard form for a vertical hyperbola centered at the origin is:
\(\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\)
Find the slopes of the asymptotes from the graph. The asymptotes are the dashed lines crossing through the origin. The slopes appear to be \(\pm \frac{b}{a}\). From the graph, the asymptotes pass through points (7, 5) and (5, 7), so calculate the slope as \(\frac{5}{7}\) or \(\frac{7}{5}\) and identify which corresponds to \(\frac{b}{a}\).
Use the slope of the asymptotes to solve for \(b\). Since \(a = 7\), and slope \(= \frac{b}{a}\), multiply the slope by \(a\) to find \(b\). Then write the standard form equation by substituting \(a^2\) and \(b^2\) into the formula.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Standard Form of a Hyperbola
The standard form of a hyperbola equation depends on its orientation. For a hyperbola centered at the origin with vertical transverse axis, the form is (y²/a²) - (x²/b²) = 1. Here, 'a' is the distance from the center to the vertices along the transverse axis, and 'b' relates to the conjugate axis. Identifying 'a' and 'b' from the graph is essential to write the equation.
Recommended video:

Asymptotes of Hyperbolas
Vertices and Center of the Hyperbola
The vertices are points where the hyperbola intersects its transverse axis, indicating the distance 'a' from the center. The center is the midpoint between the vertices, often at the origin in this problem. Knowing the coordinates of the vertices (0,7) and (0,-7) helps determine 'a' and confirms the hyperbola's vertical orientation.
Recommended video:

Foci and Vertices of Hyperbolas
Asymptotes of a Hyperbola
Asymptotes are lines that the hyperbola approaches but never touches, defined by y = ±(a/b)x for vertical hyperbolas. The slopes of the asymptotes help find 'b' once 'a' is known. The dashed lines in the graph represent these asymptotes, and their slopes can be calculated from the grid to complete the hyperbola's equation.
Recommended video:

Asymptotes of Hyperbolas

 5:59m
5:59mWatch next
Master Graph Hyperbolas NOT at the Origin with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
722
views
