Use Descartes' Rule of Signs to explain why has no real roots.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
4. Polynomial Functions
Zeros of Polynomial Functions
Problem 51
Textbook Question
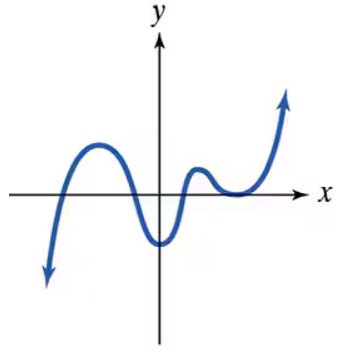
In Exercises 51–54, graphs of fifth-degree polynomial functions are shown. In each case, specify the number of real zeros and the number of imaginary zeros. Indicate whether there are any real zeros with multiplicity other than 1.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the degree of the polynomial. Since it is a fifth-degree polynomial, it has exactly 5 zeros in total (including real and imaginary zeros), according to the Fundamental Theorem of Algebra.
Step 2: Count the number of real zeros by observing where the graph crosses or touches the x-axis. In the graph, the polynomial crosses the x-axis at four points: approximately at x = -1, x = 1, x = 2, and one more point between 1 and 2 where the curve touches the x-axis but does not cross it.
Step 3: Determine the multiplicity of each real zero by analyzing the behavior of the graph at those points. If the graph crosses the x-axis, the zero has odd multiplicity (usually 1). If the graph only touches the x-axis and turns around, the zero has even multiplicity (greater than 1). Here, the zero between 1 and 2 appears to be a touch point, indicating multiplicity greater than 1.
Step 4: Calculate the number of imaginary zeros by subtracting the number of real zeros from the total number of zeros. Since the polynomial is degree 5 and there are 4 real zeros, the remaining zeros must be imaginary.
Step 5: Summarize the findings: state the number of real zeros, the number of imaginary zeros, and specify which real zeros have multiplicity greater than 1 based on the graph's behavior.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Real Zeros of a Polynomial
Real zeros of a polynomial are the x-values where the graph crosses or touches the x-axis. Each zero corresponds to a root of the polynomial equation. In the graph, these are the points where the curve intersects the x-axis.
Recommended video:

Finding Zeros & Their Multiplicity
Multiplicity of Zeros
Multiplicity refers to how many times a particular zero is repeated as a root of the polynomial. If the graph touches the x-axis and turns around, the zero has even multiplicity; if it crosses the axis, the zero has odd multiplicity. Multiplicity affects the shape of the graph near the zero.
Recommended video:

Finding Zeros & Their Multiplicity
Imaginary (Complex) Zeros
Imaginary zeros are roots of the polynomial that are not real numbers and do not appear as x-intercepts on the graph. For a polynomial of degree n, the total number of zeros (real and imaginary) is n, counting multiplicities, according to the Fundamental Theorem of Algebra.
Recommended video:

Introduction to Complex Numbers
Related Videos
Related Practice
Textbook Question
784
views
