In Exercises 31–42, solve by the method of your choice. Identify systems with no solution and systems with infinitely many solutions, using set notation to express their solution sets. x + 3y = 2 3x + 9y = 6
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
Two Variable Systems of Linear Equations
Problem 42
Textbook Question
Determine the system of equations illustrated in each graph. Write equations in standard form.
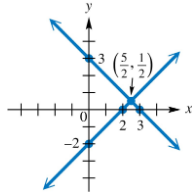
 Verified step by step guidance
Verified step by step guidance1
Identify two points on the first line. From the graph, these points are (-8, 0) and (-4, 0).
Calculate the slope of the first line using the formula \(m = \frac{y_2 - y_1}{x_2 - x_1}\). Since both points have \(y=0\), the slope is \(m = 0\).
Write the equation of the first line in slope-intercept form: \(y = 0\). Convert this to standard form: \(y = 0\) or \$0x + y = 0$.
Identify two points on the second line. From the graph, these points are (0, 10) and (0, -3).
Calculate the slope of the second line using the formula \(m = \frac{y_2 - y_1}{x_2 - x_1}\). Since both points have \(x=0\), the slope is undefined, indicating a vertical line. The equation is \(x = 0\) in standard form.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Finding the Equation of a Line from Intercepts
A line can be determined using its x- and y-intercepts by applying the intercept form of a linear equation. The formula is \( \frac{x}{a} + \frac{y}{b} = 1 \), where \(a\) and \(b\) are the x- and y-intercepts respectively. This form helps quickly write the equation when intercepts are known from the graph.
Recommended video:
Guided course

Graphing Lines in Slope-Intercept Form
Converting to Standard Form of a Linear Equation
The standard form of a linear equation is \(Ax + By = C\), where A, B, and C are integers, and A ≥ 0. After finding the equation from intercepts or slope-intercept form, rearranging terms to this form is essential for consistency and comparison of linear equations.
Recommended video:

Converting Standard Form to Vertex Form
Interpreting Graphs to Identify Systems of Equations
A system of equations consists of two or more linear equations graphed on the same coordinate plane. Understanding how to read points, intercepts, and slopes from the graph allows one to write each equation accurately and analyze their intersection points, which represent solutions to the system.
Recommended video:
Guided course

Introduction to Systems of Linear Equations

 4:27m
4:27mWatch next
Master Introduction to Systems of Linear Equations with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
668
views
