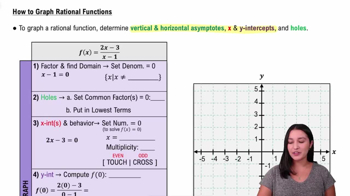
Textbook Question
Identify any vertical, horizontal, or oblique asymptotes in the graph of y=ƒ(x). State the domain of ƒ.
1063
views
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 6:24m
6:24mMaster Introduction to Asymptotes with a bite sized video explanation from Patrick
Start learning