For the given solution set {2, -1}, write a quadratic equation in a general form. 

Find the solution set for the following inequality. Express the answer in interval notation. (9x + 2)/(- 5) ≤ 3x + 2

Determine if the following relation is a function. If so, find its domain and range:

{(1, 11), (1, 22), (3, 8), (3, 10)}

Identify if the given table of x and y-values represents a function. Also, find the domain and range.

For the given conditions: Slope = - 2, passing through (- 3, - 1/3)

Write an equation for the line in Slope-intercept form by first going through the point-slope form.

For a circle with the following center and radius, find its equation (in standard form).

Center = (- 8, - 16), r = √8

Graph h(x) = 3√(x + 4) as a transformation of the square root function f(x) = √x.

Graph the absolute value function g(x) = - |5x + 5| + 3/2 as a transformation of f(x) = |5x|.

Find the value of the expression using the graph given below.

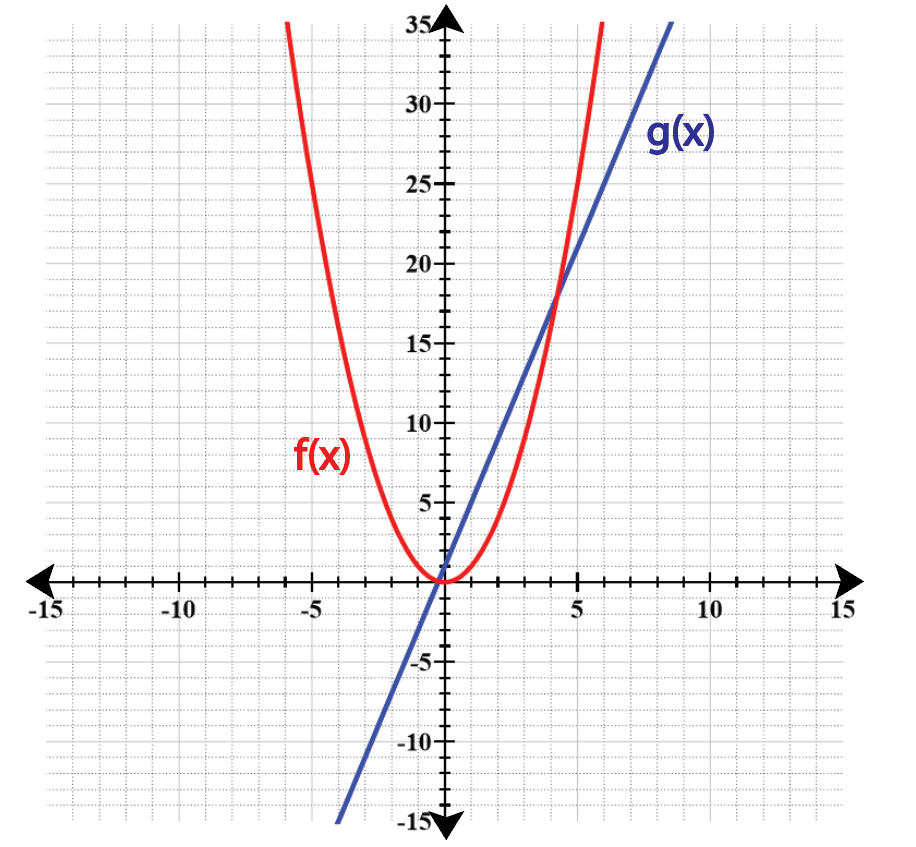
(f - g)(-2)

Given the two functions $f$ and $g$, find $fg$ and identify the domain.

$f\left(x\right)=71x-2$, $g\left(x\right)=x+10$

Find out the equation of the parabola in the vertex form for the given condition:
(a) Shape of the parabola same as f(x) = 13x² 

(b) vertex of the parabola (-1, -1)

Consider the given polynomial function and plot its graph.
ƒ(x) = (x-17)(x-29)

Find the quotient and indicate the remainder, r(x), if long division would be performed on the following.

(4x⁵ + 2x³ + 8x²) ÷ (5x² + 3)

If 1 is a zero of the following polynomial function, solve for all the other zeros. f(x) = x³ + 13x² - 14.

Determine the end behavior of the graph of the following polynomial function using the Leading Coefficient Test: $f(x)=2x^{4}+19x^{2}-3x-2$

Graph the given rational function following the seven steps. f(x)=(7x²-6x−16)/(4x²−5x)

The characteristics of the graph of a rational function f are given below. Find f(x).

x-intercepts: (0, 0)

vertical asymptotes: x = -2 and x = 2

horizontal asymptote: y = 0

Complete the given statement using the graph of the rational function in the figure shown.

As x → 6^-, f(x) →