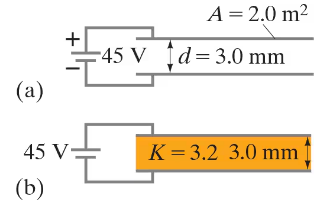
A parallel-plate capacitor has capacitance pF when there is air between the plates. The separation between the plates is mm.
(a) What is the maximum magnitude of charge that can be placed on each plate if the electric field in the region between the plates is not to exceed V/m?
(b) A dielectric with is inserted between the plates of the capacitor, completely filling the volume between the plates. Now what is the maximum magnitude of charge on each plate if the electric field between the plates is not to exceed V/m?