What nuclide is produced in the following radioactive decays?
(a) decay of
(b) decay of
(c) decay of
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: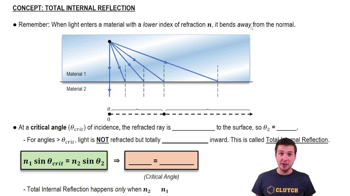



 1:37m
1:37mMaster Introduction to Physics Channel with a bite sized video explanation from Patrick
Start learning