Textbook Question
Two identical particles have equal but opposite momenta, and , but they are not traveling along the same line. Show that the total angular momentum of this system does not depend on the choice of origin.
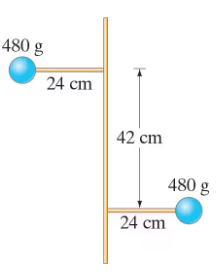
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 7:06m
7:06mMaster Angular Momentum of Objects in Linear Motion with a bite sized video explanation from Patrick
Start learning