In Exercises 17 and 18, use the table, which shows the numbers...

Question

In Exercises 17 and 18, use the table, which shows the numbers of first-time and repeat U.S. nursing students taking the National Council Licensure Examination (NCLEX-RN® exam) to pass or fail in a recent year. (Adapted from National Council Licensure Examinations)

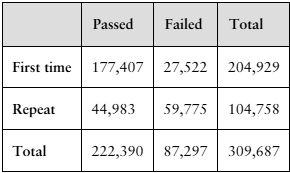
17. Find the probability that a student took the exam for the first time, given that the student failed.

Table showing the number of first-time and repeat nursing students who passed or failed the NCLEX-RN exam.

17. Find the probability that a student took the exam for the first time, given that the student failed.

Accepted Answer

Hello there. Today we're going to solve the following practice problem together. So first off, let us read the problem and highlight all the key pieces of information that we need to use in order to solve this problem. A statistics department reports the following data for students taking the final exam. Passed, failed, first time, 18,900, 4780. Repeat, 5320, 2540. What is the probability that a student was a repeat test taker, given that the student failed the exam? Awesome. So it appears for this particular prom we're asked to determine the numerical value for the probability. So we're trying to determine the probability that a student, based on the information that is provided to us by the prom itself, we're trying to determine the probability that a student was a repeat test taker, given that they failed the exam. So with that in mind, let's read off our multiple choice answers to see what our final answer might be. A is 0.347, B is 0.523, C is 0.246, and D is 0.319. Awesome. So with that in mind, our first step that we need to take in order to solve this problem is we need to calculate the total number of students who failed the exam. So using our row that denotes the failed amount of students that are first time test takers and repeat test takers, we need to take from our table 4780, so 4000. 780, and then we need to add 2540. So, when we add these two values together, we will find that they're equal to 7320. Our second step now is we need to identify the number of repeat students who failed the exam, which, according to our figure that is provided to us by the prom itself, that value once again for the amount of students who are repeat students who failed the exam was 2540 students. Our 3rd step now is we need to recall and use the conditional probability formula, which for this case, we could write it as the probability. Of a student being a repeat test taker. Given that they failed the exam, which we could write as the probability. Of repeat, which I'll denote as R given failed, which I'll denote failed as F. So we'll write this as P P parentheses R bar F. And in order to determine the, once again, the probability of a student being a repeat test taker, given that they failed the exam, once again, we're recalling how to use the conditional probability formula which, based on the information that is provided to us by the problem itself, we need to take 2000. 540, and we need to divide it by 7320. These once again we our final answer we're trying to solve for is the probability that a student was a repeat test taker, given that the student failed the exam. So, when we plug in this expression into our calculator, we will find that it's approximately equal to 0.347 when we round to three decimal places. And this is our final answer. Hooray, we did it. And this corresponds to multiple choice answer letter A, which once again is 0.347. Thank you so much for watching. Hopefully that helped, and I can't wait to see you in the next video. Bye.

Key Concepts

Conditional Probability

Joint Probability

Total Probability

Watch next