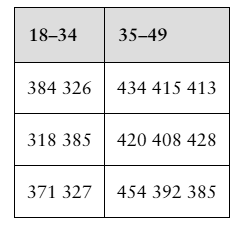
Use a table to find or estimate such that:
(Area to the left)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 5:39m
5:39mMaster Critical Values: Chi Square Distribution with a bite sized video explanation from Patrick
Start learning