What are the conditions for using a Kruskal-Wallis test?
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 25m
- 9. Hypothesis Testing for One Sample3h 57m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 24m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit2h 21m
- 14. ANOVA1h 57m
9. Hypothesis Testing for One Sample
Steps in Hypothesis Testing
Problem 10.Q.2c
Textbook Question
In each exercise,
c. find the test statistic,
In Exercises 1 and 2, use the table, which lists the distribution of educational achievement for people in the United States ages 25 and older. It also lists the results of a random survey for two additional age groups. (Adapted from U.S. Census Bureau)
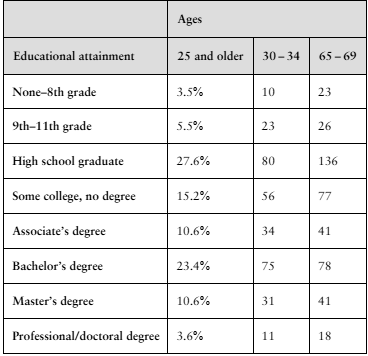
Use the data for 30- to 34-year-olds and 65- to 69-year-olds to test whether age and educational attainment are related. Use α=0.01.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Define the null hypothesis (H₀) and the alternative hypothesis (H₁). H₀: Age and educational attainment are independent. H₁: Age and educational attainment are related.
Step 2: Organize the data into a contingency table. Use the given data for the two age groups (30–34 and 65–69) and the educational attainment categories.
Step 3: Calculate the expected frequencies for each cell in the contingency table using the formula: E = (row total × column total) / grand total. This ensures the expected frequencies align with the assumption of independence.
Step 4: Compute the test statistic using the chi-square formula: χ² = Σ((O - E)² / E), where O represents the observed frequency and E represents the expected frequency for each cell.
Step 5: Compare the calculated χ² value to the critical value from the chi-square distribution table at α = 0.01 with the appropriate degrees of freedom (df = (number of rows - 1) × (number of columns - 1)). If χ² > critical value, reject H₀; otherwise, fail to reject H₀.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Test Statistic
A test statistic is a standardized value that is calculated from sample data during a hypothesis test. It measures how far the sample statistic is from the null hypothesis, expressed in terms of standard errors. Common test statistics include the z-score and t-score, which help determine whether to reject the null hypothesis based on the significance level.
Recommended video:
Guided course

Step 2: Calculate Test Statistic
Hypothesis Testing
Hypothesis testing is a statistical method used to make decisions about a population based on sample data. It involves formulating a null hypothesis (H0) and an alternative hypothesis (H1), then using sample data to determine the likelihood of observing the data if the null hypothesis is true. A significance level (α) is set to decide whether to reject H0.
Recommended video:
Guided course

Step 1: Write Hypotheses
Chi-Square Test of Independence
The Chi-Square Test of Independence is a statistical test used to determine if there is a significant association between two categorical variables. It compares the observed frequencies in each category to the frequencies expected under the assumption of independence. A significant result indicates that the variables are related, which is relevant for analyzing educational attainment across different age groups.
Recommended video:
Guided course

Independence Test

 5:12m
5:12mWatch next
Master Intro to Hypothesis Testing with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
59
views
