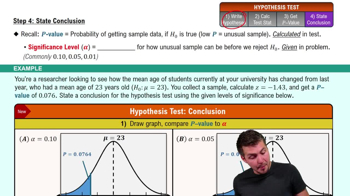
In Exercises 7–10, describe type I and type II errors for a hypothesis test of the claim.
An energy bar maker claims that the mean number of grams of carbohydrates in one bar is less than 25.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 5:12m
5:12mMaster Intro to Hypothesis Testing with a bite sized video explanation from Patrick
Start learning