Using and Interpreting Concepts
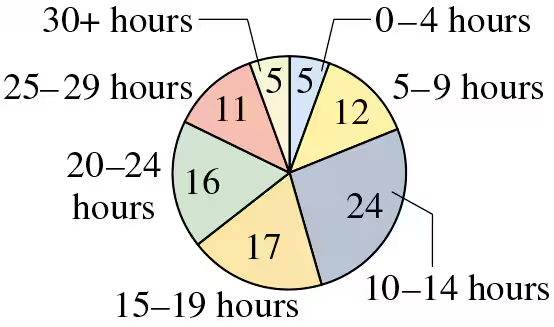
Finding the Range of a Data Set In Exercises 9 and 10, find the range of the data set represented by the graph.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 8:45m
8:45mMaster Calculating Standard Deviation with a bite sized video explanation from Patrick
Start learning