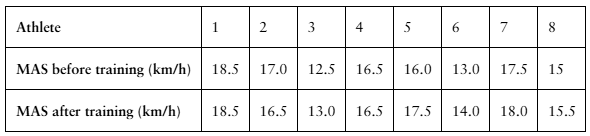
Testing the Difference Between Two Means (a) identify the clai...

Question

Testing the Difference Between Two Means (a) identify the claim and state Ho and Ha ,Assume the samples are random and dependent, and the populations are normally distributed.

Interval Training

A researcher claims that sprint interval training improves running performance in trained athletes. The table shows the maximum aerobic speed (MAS), in kilometers per hour, of trained athletes before and after six sessions of sprint interval training. At , α=0.10 is there enough evidence to support the researcher’s claim? (Adapted from National Strength and Conditioning Association)

Table comparing maximum aerobic speed of athletes before and after sprint interval training sessions.

Accepted Answer

Hi everybody, I'm glad to have you back. The next question says, a sports scientist wants to test whether a hydration supplement increases the endurance time in minutes of long-distance cyclists. The endurance time for each cyclist is recorded before and after taking the supplement. What are the null and alternative hypotheses? A null hypothesis is sub D is equal to 0, so the mean difference is equal to 0. The alternative hypothesis is that the mean difference is greater than 0. Choice B, no, is that the mean difference equals 0. And the alternative is that the main difference is less than 0. Choice C null is that the mean difference is greater than 0. Alternative is that the mean difference is equal to 0. And then choice D, the null is that the mean difference is equal to 0, and the alternative is that the mean difference does not equal 0. So we can quite easily eliminate choice C, which is that the null hypothesis is that the mean difference is greater than 0. Because we want our null hypothesis to have. A statement of equality. So we'd want to see the symbols equals less than or equal to or greater than or equal to in that null hypothesis. So, let's think about our test here. So, we're looking to see, does the supplement increase endurance time, and we're looking at samples that record before and after. So, we look at a difference of the time after, the endurance time after, and then subtract the endurance time before. We say time after. Minus time before. And if the supplement has increased endurance time, we'd want to see that being greater than 0, being positive. So if A supplement So, we can see that this is a statement of inequality, and that this is our claim. The sports scientist is testing this claim. So that means our alternative hypothesis will be based on this claim. So we can actually kind of use this to eliminate some answers. So in choice B, we see that the alternative hypothesis says that the mean difference is less than 0. This would mean that the supplement decreases endurance time. So we wouldn't want that to be our alternative hypothesis. And then in choice D that alternative hypothesis is that the mean difference does not equal zero, which would mean we would reject. Or if we reject the null hypothesis, it means we're just looking to see whether the hydration supplement changes endurance time, either increasing or decreasing it. So that also wouldn't be how we would want to express the alternative hypothesis. So, indeed, we've eliminated everything but choice A, and indeed, that is correct. So, we start with a null hypothesis of a statement of equality, and in this case, our null hypothesis would be no change. And therefore, that would indicate that that median or excuse me, mean difference is equal to 0, and that's what we have in choice A. And then we'd have our claim being that the mean difference is greater than 0, which is what's listed in choice A. So again, we're testing a claim whether a hydration hydration supplement increases endurance time. The endurance time is recorded for each cyclist before and after taking the supplement as to samples. There are 2 sample sets. What are our null on an alternative hypotheses in this case? And the answer is choice A. The null hypothesis is that the mean difference equals 0. And the alternative hypothesis is that the mean difference is greater than 0. See you in the next video.

Key Concepts

Hypothesis Testing

Dependent Samples

Significance Level (α)

Watch next