Explain how to transform a given x-value of a normally distributed variable x into a z-score.
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 25m
- 9. Hypothesis Testing for One Sample3h 57m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 24m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit2h 21m
- 14. ANOVA1h 57m
6. Normal Distribution and Continuous Random Variables
Probabilities & Z-Scores w/ Graphing Calculator
Problem 5.2.15
Textbook Question
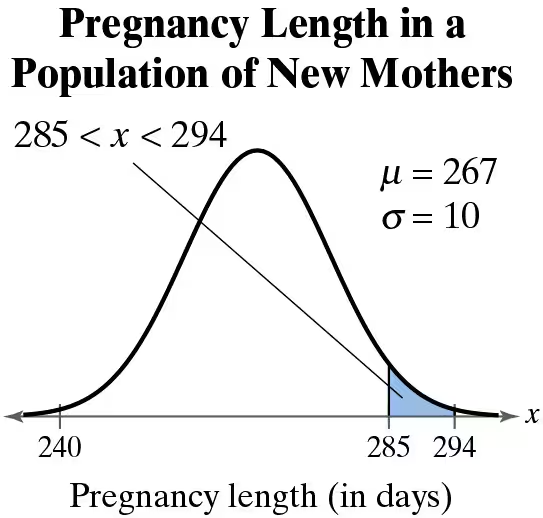
Graphical Analysis In Exercises 13–16, a member is selected at random from the population represented by the graph. Find the probability that the member selected at random is from the shaded region of the graph. Assume the variable x is normally distributed.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the key parameters of the normal distribution from the graph. The mean (μ) is given as 267 days, and the standard deviation (σ) is 10 days. The shaded region corresponds to the range 285 < x < 294.
Step 2: Convert the given range (285 < x < 294) into z-scores using the formula: . For x = 285 and x = 294, calculate the respective z-scores.
Step 3: Use a standard normal distribution table or software to find the cumulative probabilities corresponding to the calculated z-scores. The cumulative probability for z = (285 - 267)/10 and z = (294 - 267)/10 will be determined.
Step 4: Subtract the cumulative probability at z = 285 from the cumulative probability at z = 294 to find the probability of the shaded region. This gives the area under the curve between these two z-scores.
Step 5: Interpret the result as the probability that a randomly selected member of the population has a pregnancy length between 285 and 294 days.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Normal Distribution
Normal distribution is a continuous probability distribution characterized by its bell-shaped curve, defined by its mean (μ) and standard deviation (σ). In this context, the pregnancy lengths are normally distributed, meaning most values cluster around the mean, with fewer values appearing as you move away from the mean in either direction.
Recommended video:

Using the Normal Distribution to Approximate Binomial Probabilities
Probability
Probability quantifies the likelihood of an event occurring, expressed as a number between 0 and 1. In this scenario, we are interested in finding the probability that a randomly selected pregnancy length falls within a specific range (285 to 294 days), which can be calculated using the area under the normal distribution curve corresponding to that interval.
Recommended video:

Introduction to Probability
Z-scores
A Z-score indicates how many standard deviations an element is from the mean of a distribution. It is calculated using the formula Z = (X - μ) / σ. In this case, Z-scores can be used to standardize the values of 285 and 294, allowing us to find the corresponding probabilities from the standard normal distribution table.
Recommended video:
Guided course

Z-Scores From Given Probability - TI-84 (CE) Calculator

 7:09m
7:09mWatch next
Master Probability From Given Z-Scores - TI-84 (CE) Calculator with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
59
views
