Multiple Choice
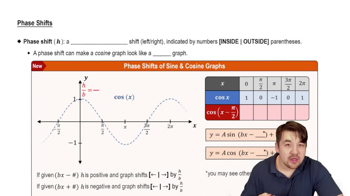
Below is a graph of the function . Determine the value of b.
806
views
3
rank
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 5:43m
5:43mMaster Introduction to Tangent Graph with a bite sized video explanation from Patrick
Start learning