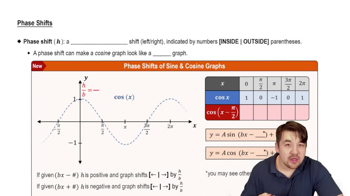
Determine an equation of the form y = a cos bx or y = a sin bx, where b > 0, for the given graph. See Example 6.
<IMAGE>
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 5:53m
5:53mMaster Graph of Sine and Cosine Function with a bite sized video explanation from Patrick
Start learning