Textbook Question
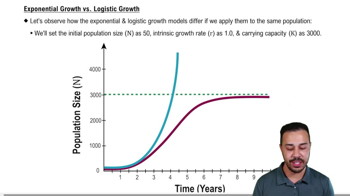
The term (K−N)/K
a. Is the carrying capacity for a population.
b. Is greatest when K is very large.
c. Is zero when population size equals carrying capacity.
d. Increases in value as N approaches K.
2215
views
50. Population Ecology
Introduction to Population Ecology
2:38 minutesProblem 6
Textbook Question
With regard to its rate of growth, a population that is growing logistically
a. Grows fastest when density is lowest
b. Has a high intrinsic rate of increase
c. Grows fastest at an intermediate population density
d. Grows fastest as it approaches carrying capacity
Verified step by step guidance1
Understand the concept of logistic growth: Logistic growth occurs when a population's growth rate decreases as the population size approaches the carrying capacity of the environment. The growth follows an S-shaped curve.
Recall the formula for logistic growth: The logistic growth model is expressed as \( \frac{dN}{dt} = rN \left(1 - \frac{N}{K}\right) \), where \( N \) is the population size, \( r \) is the intrinsic rate of increase, \( K \) is the carrying capacity, and \( \frac{dN}{dt} \) is the rate of population growth.
Analyze the growth rate at different population densities: At very low population densities (\( N \) close to 0), the term \( \left(1 - \frac{N}{K}\right) \) is close to 1, but the population size \( N \) is small, so the growth rate is low. At very high population densities (\( N \) close to \( K \)), \( \left(1 - \frac{N}{K}\right) \) approaches 0, causing the growth rate to slow down significantly.
Determine the point of fastest growth: The population grows fastest at intermediate densities, where \( N \) is neither too small nor too close to \( K \). At this point, both \( N \) and \( \left(1 - \frac{N}{K}\right) \) contribute significantly to the growth rate.
Match the correct answer to the problem: Based on the analysis, the correct answer is the option that states the population grows fastest at an intermediate population density.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Logistic Growth Model
The logistic growth model describes how a population grows in an environment with limited resources. Initially, the population grows exponentially, but as it approaches the carrying capacity of the environment, the growth rate slows down. This model is characterized by an S-shaped curve, where growth is rapid at first, slows as resources become scarce, and eventually stabilizes.
Recommended video:
Guided course
09:46
Exponential Growth vs. Logistic Growth
Carrying Capacity
Carrying capacity refers to the maximum number of individuals of a species that an environment can sustainably support. It is determined by factors such as food availability, habitat space, and competition. As a population nears its carrying capacity, the growth rate decreases, leading to a balance between birth and death rates.
Recommended video:
Guided course
06:24Estimating Earth’s Human Carrying Capacity
Population Density
Population density is the number of individuals per unit area or volume in a given habitat. It plays a crucial role in population dynamics, influencing competition for resources, reproduction rates, and mortality. In logistic growth, populations tend to grow fastest at intermediate densities, where resources are still abundant but competition is not yet limiting.
Recommended video:
Guided course
01:52Population Size & Density
Related Videos
Related Practice