Using the sample data below, run a hypothesis test on to see if there is evidence that there is a positive correlation between and with .
Table of contents
- 1. Introduction to Statistics53m
- 2. Describing Data with Tables and Graphs2h 1m
- 3. Describing Data Numerically1h 48m
- 4. Probability2h 26m
- 5. Binomial Distribution & Discrete Random Variables2h 55m
- 6. Normal Distribution & Continuous Random Variables1h 48m
- 7. Sampling Distributions & Confidence Intervals: Mean2h 8m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 20m
- 9. Hypothesis Testing for One Sample2h 23m
- 10. Hypothesis Testing for Two Samples3h 25m
- 11. Correlation1h 6m
- 12. Regression1h 59m
- 13. Chi-Square Tests & Goodness of Fit2h 7m
- 14. ANOVA1h 4m
12. Regression
Inferences for Slope
Struggling with Statistics for Business?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
Using the sample data below, create a confidence interval for to see if there is evidence that there is a positive correlation between and with .
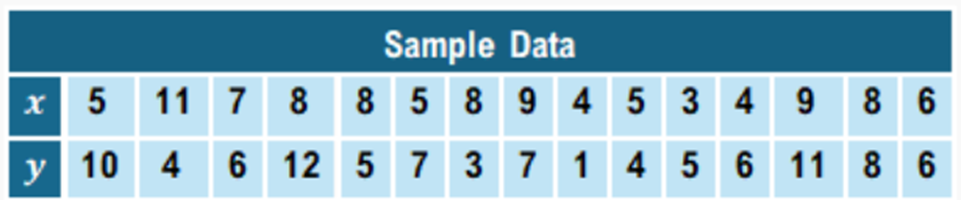
A
(−0.75,1.37); there is not enough evidence to suggest that there is a positive correlation between x and y with α=0.01.
B
(−0.75,1.37); there is enough evidence to suggest that there is a positive correlation between x and y with α=0.01.
C
(0.75,1.37); there is not enough evidence to suggest that there is a positive correlation between x and y with α=0.01.
D
(0.75,1.37); there is enough evidence to suggest that there is a positive correlation between x and y with α=0.01.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Calculate the means of the sample data for both variables $x$ and $y$. Use the formulas:
$$\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i \quad \text{and} \quad \bar{y} = \frac{1}{n} \sum_{i=1}^n y_i$$
where $n$ is the number of data points.
Step 2: Compute the slope estimate $\hat{\beta}$ of the regression line, which represents the estimated correlation between $x$ and $y$. Use the formula:
$$\hat{\beta} = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2}$$
Step 3: Calculate the standard error of the slope estimate $SE_{\hat{\beta}}$. First, find the residual sum of squares (RSS) by computing the differences between observed $y_i$ and predicted values $\hat{y}_i = \hat{\beta} x_i + \hat{\alpha}$, then use:
$$SE_{\hat{\beta}} = \sqrt{\frac{\text{RSS} / (n-2)}{\sum_{i=1}^n (x_i - \bar{x})^2}}$$
where $\hat{\alpha}$ is the intercept estimate.
Step 4: Determine the critical value $t^*$ from the $t$-distribution for a two-tailed test with significance level $\alpha = 0.01$ and degrees of freedom $df = n - 2$.
Step 5: Construct the confidence interval for $\beta$ using the formula:
$$\hat{\beta} \pm t^* \times SE_{\hat{\beta}}$$
Interpret the interval to check if it contains zero. If zero is included, there is not enough evidence to conclude a positive correlation at the $\alpha=0.01$ significance level.

 4:30m
4:30mWatch next
Master Hypothesis Test for the Slope of a Regression Line with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
