Express sinh⁻¹ x in terms of logarithms.

Find d/dx(ln(x/x²+1)) without using the Quotient Rule.

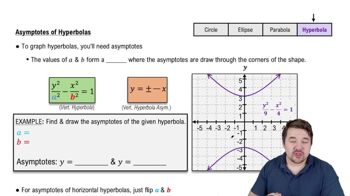
97–100. Logistic growth Scientists often use the logistic growth function P(t) = P₀K / P₀+(K−P₀)e^−r₀t to model population growth, where P₀ is the initial population at time t=0, K is the carrying capacity, and r₀ is the base growth rate. The carrying capacity is a theoretical upper bound on the total population that the surrounding environment can support. The figure shows the sigmoid (S-shaped) curve associated with a typical logistic model. <IMAGE>

{Use of Tech} Gone fishing When a reservoir is created by a new dam, 50 fish are introduced into the reservoir, which has an estimated carrying capacity of 8000 fish. A logistic model of the fish population is P(t) = 400,000 / 50+7950e^−0.5t, where t is measured in years.

c. How fast (in fish per year) is the population growing at t=0? At t=5?

7–28. Derivatives Evaluate the following derivatives.

d/dx (sin (ln x))

A calculator has a built-in sinh⁻¹ x function, but no csch⁻¹ x function. How do you evaluate csch⁻¹ 5 on such a calculator?

On what interval is the formula d/dx (tanh⁻¹ x) = 1/(1 - x²) valid?

What is the domain of sech⁻¹ x? How is sech⁻¹ x defined in terms of the inverse hyperbolic cosine?

11–15. Identities Prove each identity using the definitions of the hyperbolic functions.

tanh(−x) = −tanh x

11–15. Identities Prove each identity using the definitions of the hyperbolic functions.

cosh 2x = cosh²x + sinh²x (Hint: Begin with the right side of the equation.)