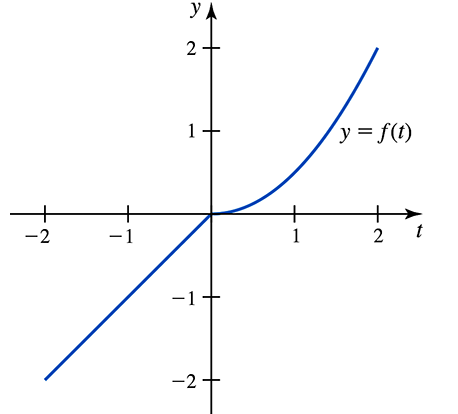
Area functions and the Fundamental Theorem Consider the function
ƒ(t) = { t if ―2 ≤ t < 0
t²/2 if 0 ≤ t ≤ 2
and its graph shown below. Let F(𝓍) = ∫₋₁ˣ ƒ(t) dt and G(𝓍) = ∫₋₂ˣ ƒ(t) dt.

(e) Evaluate F ''(―1) and F ''(1). Interpret these values.

Verified step by step guidance

Step 1: Recall the Fundamental Theorem of Calculus, which states that if F(𝓍) = ∫ₐˣ ƒ(t) dt, then F'(𝓍) = ƒ(𝓍). To find F''(𝓍), we differentiate ƒ(𝓍) with respect to 𝓍.

Step 2: Analyze the given piecewise function ƒ(t). For -2 ≤ t < 0, ƒ(t) = t. For 0 ≤ t ≤ 2, ƒ(t) = t²/2. The derivative of ƒ(t) will depend on which interval t lies in.

Step 3: Compute the derivative of ƒ(t) for each interval. For -2 ≤ t < 0, ƒ'(t) = 1 (since the derivative of t is 1). For 0 ≤ t ≤ 2, ƒ'(t) = t (since the derivative of t²/2 is t).

Step 4: Evaluate F''(𝓍) at the specified points. For F''(-1), since -1 lies in the interval -2 ≤ t < 0, use ƒ'(t) = 1. Thus, F''(-1) = 1. For F''(1), since 1 lies in the interval 0 ≤ t ≤ 2, use ƒ'(t) = t. Thus, F''(1) = 1.

Step 5: Interpret the results. F''(𝓍) represents the rate of change of the slope of F(𝓍). At 𝓍 = -1, the slope of F(𝓍) is changing at a constant rate of 1. At 𝓍 = 1, the slope of F(𝓍) is also changing at a rate of 1, but this is due to the quadratic nature of ƒ(t) in the interval 0 ≤ t ≤ 2.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Fundamental Theorem of Calculus

The Fundamental Theorem of Calculus links the concept of differentiation and integration, stating that if F is an antiderivative of f on an interval, then the integral of f from a to b is equal to F(b) - F(a). This theorem allows us to evaluate definite integrals and understand the relationship between a function and its area under the curve.

Second Derivative

The second derivative of a function, denoted as F'', measures the rate of change of the first derivative F'. It provides information about the concavity of the function: if F'' is positive, the function is concave up, and if F'' is negative, it is concave down. Evaluating the second derivative at specific points helps in understanding the behavior of the function at those points.

Definite Integral

A definite integral represents the signed area under the curve of a function f(t) from a lower limit to an upper limit. It is denoted as ∫_a^b f(t) dt and provides a numerical value that reflects the accumulation of quantities, such as area, over the specified interval. In this context, it is used to define the functions F(x) and G(x) based on the given piecewise function f(t).

Watch next

Master Fundamental Theorem of Calculus Part 1 with a bite sized video explanation from Patrick

Start learning