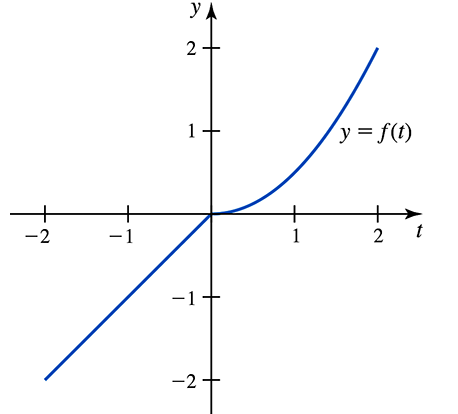
Area functions and the Fundamental Theorem Consider the function
ƒ(t) = { t if ―2 ≤ t < 0
t²/2 if 0 ≤ t ≤ 2
and its graph shown below. Let F(𝓍) = ∫₋₁ˣ ƒ(t) dt and G(𝓍) = ∫₋₂ˣ ƒ(t) dt.
(b) Use the Fundamental Theorem to find an expression for F '(𝓍) for ―2 ≤ 𝓍 < 0.