Graph the ellipse ( x − 1 ) 2 9 + ( y + 3 ) 2 4 = 1 \frac{\left(x-1\right)^2}{9}+\frac{\left(y+3\right)^2}{4}=1 9 ( x − 1 ) 2 + 4 ( y + 3 ) 2 = 1 .

everyone. In this problem, we need to graph the following ellipse based on the equation. So to solve this problem, what we can do is first determine what the orientation of the ellipse is going to be. And since I can see that our larger number in the denominator nine is underneath the x value, that means we're going to have a horizontal ellipse of some kind. And the equation for a horizontal ellipse is x minus h squared over a squared plus y minus k squared over b squared is all equal to one. So this is the general form, and we have a squared underneath x since we know it's a horizontal ellipse. Now what we need to do from here is figure out where the center of our ellipse is going to be. Well, I can see that this h corresponds with positive one. So that means horizontally we're going to be shifted over one unit. Again, see that k corresponds with this three. But notice that there is a minus or excuse me, a plus sign instead of a minus sign. And because of that, that means k is actually going to be negative three. So we need to be shifted down one, two, three units. So the center of our ellipse is going to be right about here at one, negative three. Now from here what we need to do is figure out what the size of this ellipse is going to be. And to figure this out, we can look at our equation and see these numbers in the denominator and know how they are associated with the major and minor axes. Now recall that the larger number is the major axis squared and the smaller number is the minor axis squared. So for the major axis, we can see that a squared is equal to nine, meaning that a is gonna be the square root of nine, which is three. So what I can do is go over here to our ellipse. And since I see that we're dealing with a horizontal ellipse, that means we need to go horizontally to the left and to the right three units. So I can go one, two, three units to the left, and one, two, three units to the right. Now I can also see that our minor axis is or our minor axis squared is four. So if b squared is equal to four, then that means b is going to be the square root of four, which is two. So starting from the center point, I can go up two units and I can go down two units and this will give me the two points for our minor axis. Now at this point, all I need to do is connect these outside points with a smooth curve, which looks something like that. So once we connect these points, this is going to give us the ellipse that we're looking for. And that right there is the graph of the ellipse and the answer to the problem. So thanks for watching, and let's move on.

16. Parametric Equations & Polar Coordinates

Conic Sections

Calculus

16. Parametric Equations & Polar Coordinates

Conic Sections

Struggling with Calculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

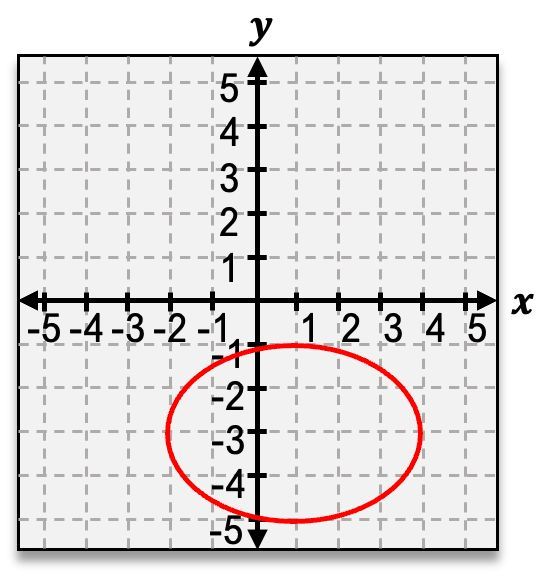
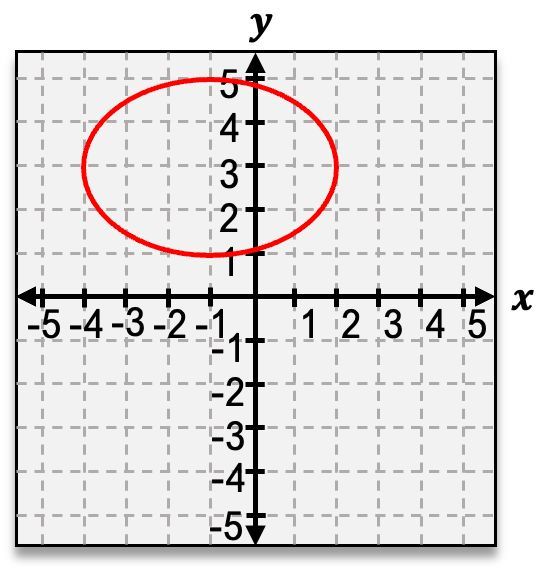
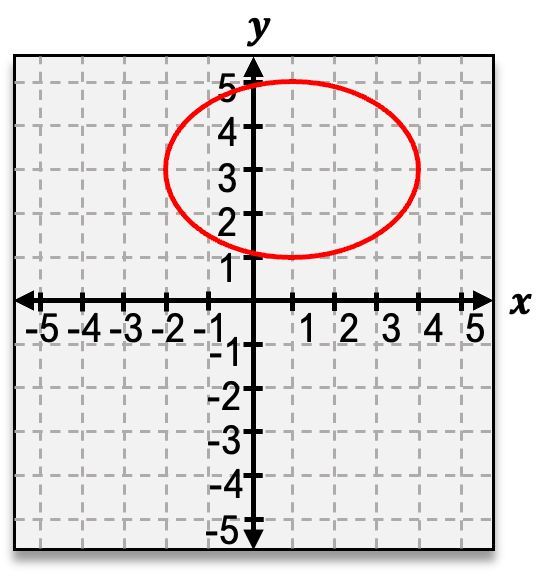
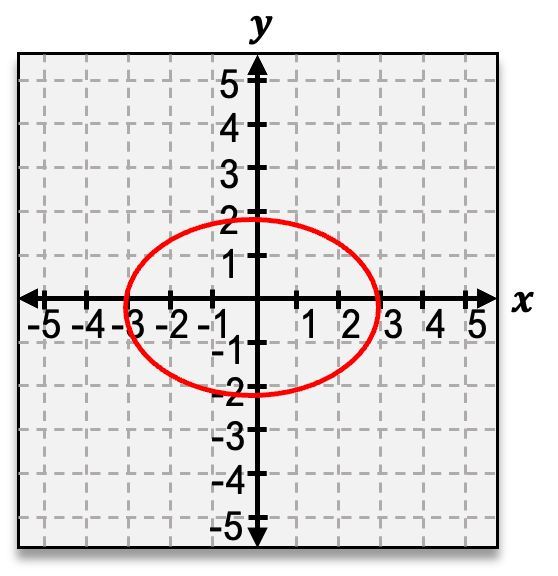
Graph the ellipse $\frac{\left(x-1\right)^2}{9}+\frac{\left(y+3\right)^2}{4}=1$ .

Graph showing an ellipse centered at (1, -3) with axes aligned to the x and y axes.

Graph showing an ellipse centered at (0, 3) with axes aligned to the x and y axes.

Graph showing an ellipse centered at (0, 1) with axes aligned to the x and y axes.

Verified step by step guidance

Step 1: Recognize the equation of the ellipse: $ \frac{(x-1)^2}{9} + \frac{(y+3)^2}{4} = 1 $. This is the standard form of an ellipse centered at $(h, k)$, where $h = 1$ and $k = -3$.

Step 2: Identify the semi-major and semi-minor axes. The denominator under $(x-1)^2$ is $9$, which corresponds to $a^2$, and $a = 3$. The denominator under $(y+3)^2$ is $4$, which corresponds to $b^2$, and $b = 2$.

Step 3: Determine the orientation of the ellipse. Since $a^2 = 9 > b^2 = 4$, the ellipse is horizontally oriented, meaning the major axis is along the x-axis.

Step 4: Plot the center of the ellipse at $(1, -3)$. From the center, move $3$ units left and right along the x-axis to mark the vertices $(1-3, -3)$ and $(1+3, -3)$, which are $(-2, -3)$ and $(4, -3)$.

Step 5: Move $2$ units up and down along the y-axis to mark the co-vertices $(1, -3-2)$ and $(1, -3+2)$, which are $(1, -5)$ and $(1, -1)$. Draw the ellipse passing through these points.